Inferential Statistics Article Critique
Review the required video
Test statistics: Crash Course statistics #26Links to an external site.
. Your instructor will post an announcement with the reference for the article to be critiqued in this assignment. Read the article assigned by your instructor and identify the research questions and/or hypotheses as they are stated.
What are the variables (sample sizes, population, treatments, etc.)?
Article:A comparative study of mental health status between players and nonplayers.
Authors: Raut Tanuja, S., & Ahmad, B. T.
Evaluate the article and critique the statistical analysis employed in the study.
Identify the specific statistical tests used. Were the tests appropriate for the situation and type of data?
Would you have included more and/or different variables? Explain your answer.
Examine the results, assumptions, interpretations, and limitations of the statistical study.
What would you have done differently? Why?
Discuss how either the statistical test(s) used in this study or the findings of this research might be useful in your future career.
Must include a separate title page with the following:
Course name and number
Must utilize academic voice. See the
Academic VoiceLinks to an external site.
resource for additional guidance.
Must include an introduction and conclusion paragraph. Your introduction paragraph needs to end with a clear statement that indicates the purpose of your paper, to critique the assigned research study article.
Must use the assigned article in addition to the course text. Additional sources are optional. You may choose to include a peer-reviewed journal article about the research design or the data analysis method used in the study.
The
Scholarly, Peer-Reviewed, and Other Credible SourcesLinks to an external site.
table offers additional guidance on appropriate source types. If you have questions about whether a specific source is appropriate for this assignment, please contact your instructor. Your instructor has the final say about the appropriateness of a specific source for a particular assignment.
To assist you in completing the research required for this assignment, view the
University of Arizona Global Campus Library Quick ‘n’ DirtyLinks to an external site.
tutorial, which introduces the University of Arizona Global Campus Library and the research process, and provides some library search tips.
Must include a separate references page that is formatted according to APA Style as outlined in the Writing Center. See the
APA: Formatting Your References ListLinks to an external site.
resource in the Writing Center for specifications.
Consider the following questions:
What are the inferential statistics used in this article?Were the proper steps of hypothesis testing followed?Your article critique paper mustDetermine what question(s) the authors are trying to answer by doing this research, the hypothesis being tested, and the concepts that were applied in this process.Evaluate the article and critique the statistical analysis employed in the study.Identify the specific statistical tests used. Were the tests appropriate for the situation and type of data?Would you have included more and/or different variables? Explain your answer.Examine the results, assumptions, interpretations, and limitations of the statistical study.Interpret the findings of the author(s) using statistical concepts.What would you have done differently? Why?Discuss how either the statistical test(s) used in this study or the findings of this research might be useful in your future career.
Keep in mind the learning objectives to help you know what concepts/terms you should be looking for in the article critique:
Examine the relationship between z scores and percentages.
Explain the concept and the testing of statistical significance.
Interpret results of t
International Journal of Sports Sciences and Fitness, Volume 5(1) 2015
A COMPARATIVE STUDY OF MENTAL HEALTH STATUS BETWEEN PLAYERS
AND NON PLAYERS
*Raut Tanuja, S. and **Bhat Tanveer Ahmad
1. Assistant Professor, P.G.T.D of Physical Education, S.G.B.A.U., Amravati, INDIA.
2. Research Scholar, Sant Gadge Baba Amravati University, Amravati, INDIA.
Email: tanuja _kathilkar @yahoo .co.in
(Received November, 28, 2014, accepted December 12, 2014)
ABSTRACT
This paper attempts to conduct a comparative study of Mental Health Status between Players
and Non Players of Amravati City. Researchers took 20 Players and 20 non players for the
present study and also age raging from 18-28 years. The mental health inventory (MHI-38)
was applied for the collection of data. The inventory included five mental health variables i,e
Anxiety, Depression, Loss Of Behaviour, Positive Affect, Emotional Ties and Life
Satisfaction. The subjects were selected by using simple random sampling method. In this
study data were analyzed and interpreted with the help of statistical term ‘t’ test. The findings
of the study shows that excepting life satisfaction variable of mental health status of players
were better than non players.
Key words: Mental Health, Anxiety, Depression, Loss Of Behaviour, Positive Affect.
INTRODUCTION
Mental health is more than the absence of a mental health condition or illness: it is a
positive sense of well-being, or the capacity to enjoy life and deal with the challenges we
face. Mental health impacts each and every one of us. We all have mental health, just as we
all have physical health. People living with a mental health issue or condition can experience
positive mental health, and an individual may experience poor mental health without a mental
health condition. Mental health is not fixed. It is influenced by a range of factors, including
our life experiences, workplace or other environments, and the social and economic
conditions that shape our lives. Mental and physical health is fundamentally linked. There are
multiple associations between mental health and physical conditions that significantly impact
people’s quality of life. The World Health Organization (WHO) defines: health as a state of
complete physical, mental and social well-being and not merely the absence of disease or
109
International Journal of Sports Sciences and Fitness, Volume 5(1) 2015
infirmity. The WHO states that “there is no health without mental health. Mental health is the
“psychological state of someone who is functioning at a satisfactory level of emotional and
behavioural adjustment”. Mental health may include an individual’s ability to enjoy life, and
create a balance between life activities and efforts to achieve psychological resilience. WHO
states that the mental well-being of an individual is encompassed in the realization of their
abilities, coping with normal stresses of life, productive work and contribution to their
community. A person struggling with his or her behavioural health may face
stress, depression, anxiety, relationship problems, addiction, or learning disabilities, mood
disorders, or other psychological concerns an age behavioural. Physical activity is good for
our mental health. Experts believe that exercise releases chemicals in your brain that make
you feel good. Regular exercise can also boost our self-esteem and help us in concentrating,
sleep, look and feel better. Leading an active life can help raise your self-worth and improve
our confidence. It can help us feel valued – and value our self. Exercise and physical activity
can provide something worthwhile in our life. Something that we really enjoy, that gives us a
goal to aim for and a sense of purpose.
There are some benefits of Physical Activities:
less tension, stress and mental fatigue
a natural energy boost
improved sleep
a sense of achievement
focus in life and motivation
less anger or frustration
a healthy appetite
better social life
having fun.
After going through literature researcher think that, if physical activities can improve
the mental wellbeing of a person then players could have good mental health status than the
non player’s .Therefore researcher had taken a study entitled as Comparative Study of Mental
Health Status between Player and Non Player.
110
International Journal of Sports Sciences and Fitness, Volume 5(1) 2015
METHODOLOGY
The main purpose of this study was to compare the mental health status of player and
non player. For this study 20 male players who represented inter university in any game & as
a non player 20 Male college students were selected from affiliated colleges of SGB
Amravati (M.S.) of Amravati city. For the collection of data simple random sampling method
are used. The data were collected by administered the standard mental health inventory
(MHI-38) on respective groups of player and non players .In this inventory five factors of
mental health was measured (i.e. anxiety, depression ,loss of behaviour, positive affect,
emotional ties life satisfaction ).Analysis of data was done with the help of “t” test. Analysis
is shown in the following table.
RESULTS AND DISCUSSION
TABLE 1
A Comparison of Scores of Mental Health Status (Anxiety, Depression, Loss Of
Behaviour, Positive Affect, Emotional Ties and Life Satisfaction) between Players and
non players
Variables
Group
Mean
S.D
M.D
Calculated
‘t’
Anxiety
Players
Non
40.65
3.39
46.35
3.29
15.32
1.39
5.7
3.91*
3.63
7.49*
4.05
4.86*
Players
Depression
Players
Non
18.95
1.64
40.2
2.74
Players
Loss Of
Players
Behaviour
Non
44.25
2.84
46.7
3.84
Players
Positive
Players
111
International Journal of Sports Sciences and Fitness, Volume 5(1) 2015
Affect
Non
40.2
2.70
10.05
0.99
6.5
2.67*
5.55
9.31*
1.95
1.27
Players
Emotional
Players
Ties
Non
4.5
1.15
4.4
1.12
Players
Life
Players
Satisfaction
Non
2.45
1.05
Players
*Significant at .05 level
“t”.05 (38) = 2.0168
It is depicted from the Table 1 that the mean of (Anxiety) of player =40.65 and non
players =46.35, mean of (Depression) of player =15.32 and non players =18.95, mean of
(Loss Of Behaviour) of player =40.2 and non players =44.25, mean of (Positive Affect) of
player =46.7 and non players =40.2, the mean of (Emotional Ties) of player =10.05 and non
players =4.5, and also mean of (Life Satisfaction) of player =4.4 and non players =2.45. It
shows that there is a mean difference in all six components of mental health status. To see
these differences are significant are not at 0.05 level. The researcher calculated ‘t test .On the
bases of this there is significant difference between all five components of mental health
status of players and non players i,e Anxiety, Depression, Loss Of Behaviour, Positive Affect
and Emotional Ties. There is only one variable Life Satisfaction there is no significance
difference between players and non players. That means players are having good mental
health status as compared to non players.
112
International Journal of Sports Sciences and Fitness, Volume 5(1) 2015
Figure 1
Graph Comparison of Scores of Mental Health Status (Anxiety, Depression, Loss Of
Behaviour, Positive Affect, Emotional Ties and Life Satisfaction) between Player and
non players
50
45
40
35
30
25
20
15
10
5
0
CONCLUSION
Players are having better mental health status than non players. Over all mental health
status shows that there is significant difference in five variables of mental health status i,e
Anxiety, Depression, Loss Of Behaviour, Positive Affect, Emotional Ties in between players
and non players. Only in Life Satisfaction variable of mental health status non players are
better than players. But this difference is not significant. Being mentally healthy doesn’t
mean never going through bad times or experiencing mental problems. We all go through
disappointments, loss, and change. And while these are normal parts of life, they can still
cause sadness, anxiety, and stress. The difference is that people with good mental health have
an ability to bounce back from adversity, trauma, and stress. This ability is called resilience.
People who are mentally healthy have the tools for coping with difficult situations and
maintaining a positive outlook. They remain focused, flexible, and creative in bad times as
well as good. One of the key factors in resilience is the ability to balance stress and our
emotions. The capacity to recognize our emotions and express them appropriately helps you
avoid getting stuck in depression, anxiety, or other negative mood states. Another key factor
113
International Journal of Sports Sciences and Fitness, Volume 5(1) 2015
is having a strong support network. Having trusted people you can turn to for encouragement
and support will boost your resilience in tough times. Taking care of our body is a powerful
first step towards mental health. The mind and the body are linked. When we improve our
physical health, we’ll automatically experience greater mental health.
REFERENCES
Alston (2000). “The Physical Fitness Programme of High School Girls on Three Physical
Fitness Test. Completed Research in Health, Physical Education and Recreation”.
Elgar, K., and Chester, A. (2007). The mental health implication of maternal employment
Australian Journal for the Advancement of Mental Health, 6. P. 1-9.
Hakkinen (2004). “Association of Physical Fitness with Health-Related Quality of Life in
Finnish Young Men. Online Journal of Health and Quality of Life Outcomes”.
Hunsicker (2001). “AAPHER Youth Fitness Test Manual Revised. American Alliance for
Health, Physical Education, and Recreation, Washington, D.C.
Jagdish and Srivastava, A. K. (1983). Mental Health Inventory. Varanasi Manavaigyanik
Sansthan.
Morgan, W. P. (1984). Selected psychological factors limiting performance: A mental health
model. American Academy of Physical Education Papers, 18. P. 70-80.
114
Copyright of International Journal of Sports Sciences & Fitness is the property of
International Journal of Sports Sciences & Fitness and its content may not be copied or
emailed to multiple sites or posted to a listserv without the copyright holder’s express written
permission. However, users may print, download, or email articles for individual use.
The Standard Normal
Distribution and z Scores
3
Keren Su/Corbis
Chapter Learning Objectives
After reading this chapter, you should be able to do the following:
1. Identify the characteristics of the standard normal distribution.
2. Demonstrate the use of the z transformation.
3. Determine the percent of a population above a point, below a point, and between two points on
the horizontal axis of a normal distribution.
4. Calculate z scores using Excel.
5. Describe alternative standard scores.
6. Demonstrate the use of the modified standard score.
61
© 2016 Bridgepoint Education, Inc. All rights reserved. Not for resale or redistribution.
tan82773_03_ch03_061-090.indd 61
3/3/16 9:56 AM
Introduction
Introduction
The data that describe characteristics of groups come from either samples or populations,
explained in the first two chapters. By way of reminder, recall that populations include all possible members of any specified group. All university students, all psychology majors, all residents of Orange County, and all left-handed male tennis players in their 20s are each descriptions of a population. We rely on Greek letters, such as µ for the mean and σ for the standard
deviation, to distinguish population parameters from the statistics that describe samples.
(The word parameter indicates a characteristic of a population.) Remove one or more individuals from any population, and the resulting group is a sample.
As we were describing populations, we noted that some are “normally distributed.” These
characteristics indicate normality: (a) data distributions are symmetrical, (b) all the measures of central tendency have very similar values, and (c) the value of the standard deviation
is about one-sixth of the range.
Data normality does not simply mean that the frequency distribution will appear as a bellshaped curve; it means that predictable proportions of the entire population will occur in
specified regions of the distribution, and this holds for all normal data distributions. For example, the region under a normal curve from the mean of the population to one standard deviation below the mean always includes 34.13% of the area under the curve. Because normal
distributions are symmetrical, from the mean to one standard deviation above the mean also
includes 34.13%, so from 11σ or 21σ includes about 68.26% of the area under the curve
in any normally distributed population. As long as the data are normally distributed, those
percentages hold true. Since many mental characteristics are normally distributed, researchers can know a good deal about such a characteristic without actually gathering the data
and doing the analysis. Whether the characteristic is intelligence, achievement motivation,
anxiety, or any other normally distributed characteristics, the proportion of the distribution
within 11 or 21 standard deviation from the mean will be the same:
• If a particular intelligence scale has µ 5 100 and σ 5 15, about 68% of any general
population will have intelligence scores between 85 and 115.
• Likewise, if an achievement motivation scale has µ 5 40 and σ 5 8, about 2/3 of any
population will have achievement motivation scores from 32 to 48.
• And for an anxiety measure with µ 5 25 and σ5 5, about 68% of any general population will have scores between 20 and 30.
The consistency in the way so many characteristics are distributed affords a good deal of
interpretive power. Anyone who needs information about the likelihood of individuals scoring in certain areas of a distribution has an advantage when data are normally distributed.
In addition to the 68% of any general population likely to score between 11σ and 21σ,
• from µ to 12σ is about 47.72% of the population, so about 95% (2 3 47.72) of
the people in any general population will have intelligence scores between
70 (100 2 30) and 130 (100 1 30).
• from 13σ (49.87%) to 23σ includes nearly everyone in any normally distributed
population (2 3 49.87 5 99.74).
These observations emphasize that, sometimes, isolated bits of data can be quite informative.
When a 12-year-old with an intelligence score of 170 pops up on YouTube, it is immediately
© 2016 Bridgepoint Education, Inc. All rights reserved. Not for resale or redistribution.
tan82773_03_ch03_061-090.indd 62
3/3/16 9:56 AM
Section 3.1
A Primer in Probability
apparent that this is a very unusual child. An intelligence score of that magnitude is about
4.667σ (170 2 100 5 70; 70 4 15 5 4.667) beyond the mean of the general population. If
from 13σ to 23σ includes more than 99% of the population, from 14.667σ to 24.667σ must
include all but the utmost extreme scores. We obtain an even better context for how common
(or uncommon) particular measures may be when we can determine the precise probability
of their occurrence.
3.1 A Primer in Probability
Scholars, data analysts, and in fact people on the whole are rarely interested in outcomes that
occur every time. If everyone had an intelligence score of 170, no one would pay any attention
to someone with such a score. The fact that we know it to be uncommon is what piques our
curiosity.
If we are not interested in events that always occur, neither do we closely follow events that
never occur. If no one had ever had an intelligence score of 170, probably no one would wonder about what such a score means for the person who has it. The things that occur some
of the time, however, intrigue us. The “some of the time” indicates that the event has some
probability, or likelihood, of occurrence.
• What is the probability that those newlyweds will divorce?
• How likely is Germany to win the World Cup?
• What is the probability that an earthquake will occur on a particular day for someone who lives near the San Andreas Fault?
• What is the probability of an IRS audit for one taxpayer?
Because all of the items listed have happened in the past and because their occurrence is
important to at least someone, people are interested in the probability of those occurrences
whether or not they use the language of probability. When stated numerically, probability values range from 0 to 1.0. Something with a probability of zero (p 5 0) never occurs.
On the other hand, p 5 1.0 indicates that the event
occurs every time, and p 5 0.5 indicates that the
event occurs 50% of the time.
As that last point indicates, percentages can be converted to probability values. Dividing the percentage of times an event occurs by 100 indicates the
associated probability of the event.
Returning to the intelligence scores, we see
that because about 68% of the population has
intelligence scores between 85 and 115, the
probability (p) that someone selected at random from the general population will have a
score somewhere between 85 and 115 is 0.68
(68.26/100, if the result is rounded to two decimal
places).
Joseph Sohm/Visions of America/Corbis
The probability that something will
occur, such as how likely it is that our
favorite baseball team will win the
World Series, intrigues us and is an
important component in the decisionmaking process.
© 2016 Bridgepoint Education, Inc. All rights reserved. Not for resale or redistribution.
tan82773_03_ch03_061-090.indd 63
3/3/16 9:57 AM
Section 3.2
The Standard Normal Distribution
What is the probability that someone selected at random from the general population will
have an intelligence score of 100 or lower? Because 100 is the mean for intelligence scores,
and because 50% of the population occur at the mean or below, p 5 0.5.
What is the probability that someone selected at random will have an intelligence score higher
than 115? First, we noted earlier that 34.13% of the population falls between the mean, µ, and
one standard deviation above the mean at σ 5 11.0 in any normally distributed population.
In terms of intelligence score values, that is the region between scores of 100 and 115. Since
50% of any normally distributed population will occur at the mean and above, if we subtract
from 50% that portion between the mean and one standard deviation above the mean, the
remainder will be the portion of the distribution above 115: 50% 2 34.13% 5 15.87%; that
is, 15.87% of all intelligence scores in a normally distributed population will occur above
115. Dividing by 100 (15.87/100 5 0.1587) and rounding the result to two decimal places
produces the probability p 5 0.16.
By the same logic, because a score of 85 is one standard deviation below the mean, the probability p 5 0.16 means that someone selected at random from the population will score below
85. If we combine the two outcomes, the probability is p 5 0.32 that someone from the population will score either below 85 or above 115.
Consider the number line shown in Figure 3.1.
Figure 3.1: Standard deviations for intelligence scores
The number line shows the portion of scores that fall within two standard deviations above and
below the mean. If M 5 100, we can know the probability of someone scoring below 85 or above 115.
34%
16%
–2σ
–1σ
70
85
34%
M
100
Intelligence scores
16%
+ 1σ
+ 2σ
115
130
If this number line represents all intelligence scores ranging from two standard deviations
below to two standard deviations above the mean, we can see the percentages of the population that will have scores in the designated areas. Using the percentages and dividing by 100
indicates the probability of a score in any of the designated areas.
Recall that the lowest probability for any value is zero (p 5 0). If p 5 0, then the event or outcome never occurs. There is no such thing as a negative probability.
3.2 The Standard Normal Distribution
Not all populations are normally distributed. Home sales are usually reported in terms of the
median price of a home, and salary data are likewise reported as median values. Those cases
© 2016 Bridgepoint Education, Inc. All rights reserved. Not for resale or redistribution.
tan82773_03_ch03_061-090.indd 64
3/3/16 9:57 AM
Section 3.2
The Standard Normal Distribution
use the medians because the related populations
are very unlikely to be normally distributed and,
as a measure of central tendency, medians are less
affected by extreme values than are means. A few
very high salaries or home values create positive
skew in the resulting distribution. In contrast, when
it comes to, say, mental characteristics such as intelligence, achievement motivation, problem-solving
ability, verbal aptitude, reading comprehension, and
so on, population data are often normally distributed.
Hello Lovely/Corbis
Although there are many normal distributions all
When evaluating information about
having the same proportions, each has different
people’s characteristics, keep in
descriptive values. An intelligence test might have
mind that data are often normally
µ 5 100 and σ 5 15 points. A nationally adminisdistributed.
tered reading test might have a mean of 60 and a
standard deviation of 8. These different parameters
can make it difficult to compare one individual’s performance across multiple measures. As
one author noted regarding scores from the Wechsler Intelligence Test for Children (WISC),
“A raw score of 5 on one [sub]test will not have the same meaning as a raw score 5 on another
[sub]test” (Brock, 2010).
One way to resolve this interpretation problem is to convert the scores from different distributions into a common metric, or measurement system. If researchers alter scores from different
distributions so that they both fit the same distribution, they can compare scores directly. A
researcher can compare them directly to determine, for example, on which test an individual
scored highest. Such comparisons are one of the purposes of the standard normal distribution.
The standard normal distribution looks like all other normal distributions—from the mean to
11 standard deviation includes 34.13% of the distribution, for example. What separates it
from the others is that in the standard normal distribution, the mean is always 0, and the
standard deviation is always 1.0 (Figure 3.2). Other distributions may have fixed values for
their means and standard deviations, but here µ is always 0 and σ is always 1.0.
Figure 3.2: The standard normal distribution
In the standard normal distribution, the mean is always 0, and the standard deviation is always 1.0.
The Mean = 0
The Standard Deviation = 1.0
–3
–2
–1
0
+1
+2
+3
© 2016 Bridgepoint Education, Inc. All rights reserved. Not for resale or redistribution.
tan82773_03_ch03_061-090.indd 65
3/3/16 9:57 AM
The Standard Normal Distribution
Section 3.2
The Standard Normal, or z, Distribution
Although various normal distributions have different means and standard deviations, they all
mirror each other in terms of how much of their populations occur in particular regions. The
standard normal distribution’s advantage is that the proportions of the whole that occur in the
various regions of the distribution have been calculated. That means that if data from any normal distribution are made to conform to the standard normal distribution, we can answer questions about what is likely to occur in virtually any area of the distribution, such as how likely it
is to score 2.5 standard deviations below the mean on a particular test, or what percentage of
the entire population will likely occur between two specified points. All such questions can be
answered when adapting normal data to the characteristics of the standard normal distribution.
Individual scores in the standard normal distribution are called z scores, which is why the
standard normal distribution is often called “the z distribution.” The formula used to turn
scores from any normal distribution into scores that conform to the standard normal distribution is the z transformation:
Formula 3.1
z5
x2M
s
where z is a score in the standard normal distribution, x is the score from the original distribution (often called a “raw” score), M is the mean of the scores before the original distribution, and s is the standard deviation of the scores from the original distribution.
Because normality is characteristic of only very large groups, samples will rarely be normal.
However, we can apply the z transformation to sample data when there is reason to believe
that the population from which the sample was drawn is normally distributed. This is what
Formula 3 reflects. The M and s indicate that the data involved are sample data. In those situations where an analyst has access to population data—a social worker has all the data for
those served by Head Start in a particular county, for example—µ replaces M and σ replaces
s in the formula. With either sample or population data, the transformation is from data that
can have any mean and standard deviation to a distribution where the mean will always equal
0 and the standard deviation will always equal 1.0.
To turn raw scores into z scores, perform the following steps:
1. Determine the mean and standard deviation for the data set.
2. Subtract the mean of the data set from each score to be transformed.
3. Divide the difference by the standard deviation of the data set.
For example, consider a psychologist interested in the level of apathy among potential voters
regarding mental health issues that affect the community. Scores on the Summary of WHo’s Apathetic Test (the SoWHAT for short), an apathy measure, are gathered for 10 registered voters:
5, 6, 9, 11, 15, 15, 17, 20, 22, 25
What’s the z score for someone who has an apathy score of 11?
• Verify that for these 10 scores, M 5 14.5 and s 5 6.737.
© 2016 Bridgepoint Education, Inc. All rights reserved. Not for resale or redistribution.
tan82773_03_ch03_061-090.indd 66
3/3/16 9:57 AM
Section 3.2
The Standard Normal Distribution
• The z score equivalent for an apathy score of 11 is
z5
x2M
11 2 14.5
5
5 20.5195
s
6.737
An apathy score of 11 translates into a z score of 20.5195. Because the mean of the z distribution is 0 and the standard deviation in the z distribution is 1.0, where would a score of
20.5195 occur on the horizontal axis of the data distribution? It would be a little over half a
standard deviation below the mean, right? Figure 3.3 shows the z distribution and the point
about where a raw score of 11 occurs in this distribution once it is transformed into a z score.
It is important to know that the z transformation does not make data normal. Calculating z
scores does not alter the distribution; it just makes them fit a distribution where the mean is
0 and the standard deviation is 1.0. Evaluating skew and kurtosis must allow the analyst to
assume that the data are normal before using the z transformation.
With a mean of 0 in the standard normal distribution, half of all z scores—all the scores below
the mean—are going to be negative. A raw score of 11 from the SoWHAT data is lower than
the mean, which was M 5 14.5, so it has a negative z value (20.5195).
Besides indicating by its sign whether the z score is above or below the mean, the value of
the z score indicates how far from the mean the z score is in standard deviations. If a score
had a z value of 1.0, it would indicate that the score is one standard deviation above the
mean. The z score for the raw score of 11 was 20.5195,
indicating that it is just over half a standard deviation
below the mean. This ease of interpretation is one of
Try It!: #1
the great values of z scores: the sign of the score indiHow many standard deviations from
cates whether the associated raw score was above or
the mean of the distribution is a z score
below the mean, and the value of the score indicates
of 1.5?
how far from the mean the raw score falls, in standard
deviation units (Fischer and Milfont, 2010).
Figure 3.3: Location of a score on the z distribution
Half of all z scores will fall below the mean, resulting in a negative value. A score of z 5 20.5195 is
slightly less than one-half a standard deviation below the mean.
–3z
–2z
–1z
0
+1z
+2z
+3z
z = – 0.5195
© 2016 Bridgepoint Education, Inc. All rights reserved. Not for resale or redistribution.
tan82773_03_ch03_061-090.indd 67
3/3/16 9:57 AM
Section 3.2
The Standard Normal Distribution
Comparing Scores from Different Instruments
Consider another application of the standard normal distribution. A counselor has intelligence and reading scores for the same person and wishes to know on which measure the
individual scored higher. Table 3.1 shows the data for the two tests. On the intelligence test,
the individual scored 105, and on the reading test, the individual scored 62.
Table 3.1: Reading and intelligence test results
Test
Mean
Standard deviation
Intelligence
100
15
Reading
60
8
If the counselor transforms both scores to make them fit the standard normal distribution,
they can be compared directly.
The z for the intelligence score is
z5
x2M
105 2 100
5
5 0.333
s
15
The z for the reading test score is
z5
x2M
62 2 60
5
5 0.250
s
8
The intelligence score of 105 and the reading score of 62 are difficult to compare because
they belong to different distributions with different means and standard deviations. When
both are transformed to fit the standard normal distribution, an analyst can directly compare
scores. The larger z value for intelligence makes it clear that individual scored higher in intelligence than in reading.
Expanding the Use of the z Distribution
Because the standard normal distribution is a normal distribution, we know that predictable
proportions of its population will occur in specific areas. As we noted earlier, however, those
proportions are known in great detail for the z distribution because this population is so
often used to answer detailed questions about the likelihood of particular outcomes. Table
3.2 indicates how much of the entire population is above or below all of the most commonly
occurring values of z. So, by transforming scores from other distributions to fit the z distribution, we can use what we know about this population to answer questions about scores from
any normal distribution.
Not all tables for z values are alike. Probably as a matter of the developer’s preference, some
tables indicate the percentage of the population below a point. Some indicate the percentage
between a point and the mean of the distribution. Some indicate the probability of scoring
in a particular area, and so on. This particular table indicates the proportion of the population between the specified value of z and the mean of the distribution. (Table 3.2 is listed as
Table B.1 in Appendix B.)
© 2016 Bridgepoint Education, Inc. All rights reserved. Not for resale or redistribution.
tan82773_03_ch03_061-090.indd 68
3/3/16 9:57 AM
Section 3.2
The Standard Normal Distribution
Table 3.2: The z table
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
1.1
0.00
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
0.0000
0.0040
0.0080
0.0120
0.0160
0.0199
0.0239
0.0279
0.0319
0.0359
0.0398
0.0793
0.1179
0.1554
0.1915
0.2257
0.2580
0.2881
0.3159
0.3413
0.3643
0.0438
0.0832
0.1217
0.1591
0.1950
0.2291
0.2611
0.2910
0.3186
0.3438
1.7
1.8
1.9
2.0
2.1
2.2
2.3
2.4
2.5
2.6
2.7
2.8
2.9
3.0
0.4554
0.4641
0.4713
0.4772
0.4821
0.4861
0.4893
0.4918
0.4938
0.4953
0.4965
0.4974
0.4981
0.4987
0.2642
0.2939
0.3212
0.3461
0.2357
0.2673
0.2967
0.3238
0.3485
0.2054
0.2389
0.2704
0.2995
0.3264
0.3508
0.1736
0.2088
0.2422
0.2734
0.3023
0.3289
0.3531
0.1406
0.1772
0.2123
0.2454
0.2764
0.3051
0.3315
0.3554
0.1064
0.1443
0.1808
0.2157
0.2486
0.2794
0.3078
0.3340
0.3577
0.0714
0.1103
0.1480
0.1844
0.2190
0.2517
0.2823
0.3106
0.3365
0.3599
0.0753
0.1141
0.1517
0.1879
0.2224
0.2549
0.2852
0.3133
0.3389
0.3621
0.3770
0.3790
0.3810
0.3830
0.4049
0.4066
0.4082
0.4099
0.4115
0.4131
0.4147
0.4162
0.4177
0.4207
0.4452
0.2324
0.2019
0.1700
0.1368
0.1026
0.0675
0.3749
0.4192
1.6
0.1985
0.1664
0.1331
0.0987
0.0636
0.3729
1.4
0.4332
0.1628
0.1293
0.0948
0.0596
0.3708
0.3869
1.5
0.1255
0.0910
0.0557
0.3686
0.3849
0.4032
0.0871
0.0517
0.3665
1.2
1.3
0.0478
0.4345
0.4463
0.4564
0.4649
0.4719
0.4778
0.4826
0.4864
0.4896
0.4920
0.4940
0.4955
0.4966
0.4975
0.4982
0.4987
0.3888
0.4222
0.4357
0.4474
0.4573
0.4656
0.4726
0.4783
0.4830
0.4868
0.4898
0.4922
0.3907
0.4236
0.4370
0.4484
0.4582
0.4664
0.4732
0.4788
0.4834
0.4871
0.4901
0.4495
0.4591
0.4671
0.4738
0.4793
0.4838
0.4875
0.4904
0.4957
0.4959
0.4977
0.4977
0.4988
0.4988
0.4967
0.4968
0.4982
0.4983
0.4987
0.4382
0.4927
0.4943
0.4976
0.4251
0.4925
0.4941
0.4956
0.3925
0.3944
0.4265
0.4394
0.4505
0.4599
0.4678
0.4744
0.4798
0.4842
0.4878
0.4906
0.4929
0.4945
0.4946
0.4969
0.4970
0.4984
0.4984
0.3962
0.4279
0.4406
0.4515
0.4608
0.4686
0.4750
0.4803
0.4846
0.4881
0.4909
0.4931
0.4948
0.4960
0.4961
0.4978
0.4979
0.4989
0.4989
0.3980
0.4292
0.4418
0.4525
0.4616
0.4693
0.4756
0.4808
0.4850
0.4884
0.4911
0.3997
0.4306
0.4429
0.4535
0.4625
0.4699
0.4761
0.4812
0.4854
0.4887
0.4913
0.4932
0.4934
0.4962
0.4963
0.4949
0.4441
0.4545
0.4633
0.4706
0.4767
0.4817
0.4857
0.4890
0.4916
0.4936
0.4952
0.4974
0.4972
0.4973
0.4985
0.4985
0.4986
0.4989
0.4319
0.4951
0.4971
0.4979
0.4015
0.4964
0.4980
0.4981
0.4990
0.4990
0.4986
Source: StatSoft. (2011). Electronic Statistics Textbook. Tulsa, OK: StatSoft. Retrieved from http://www.statsoft.com/textbook/distribution
-tables/#z
© 2016 Bridgepoint Education, Inc. All rights reserved. Not for resale or redistribution.
tan82773_03_ch03_061-090.indd 69
3/3/16 9:57 AM
Section 3.2
The Standard Normal Distribution
The z value calculation for a SoWHAT score of 11 rounded to 4 decimal values for the sake
of the illustration. The table rounds z values to just two decimals, so from this point forward,
round z values to two decimals when using the table. Rounding makes the z value for a raw
score of 11 5 20.52.
To interpret the z score, read the whole numbers and the tenths (the tenths are the first value
to the right of the decimal) vertically down the left margin of the table. For the hundredths
(the second value to the right of the decimal), move from left to right across the columns at
the top of the table.
1. Read down the left margin to the line indicating 0.5.
2. Read across the top to the column indicating 0.02.
3. The table value where row and column intersect is 0.1985. This value is the
proportion (out of a total of 1.0) of any normally distributed population that will
occur between z 5 0.52 and the population’s mean.
4. To determine the percentage of the distribution between z 5 20.52 and the mean,
multiply the table value by 100: 100 3 0.1985 5 19.85% of the distribution is
between 20.52 and the population mean.
Note that all the z values in Table 3.2 are positive. Our z score from the SoWHAT score was
actually negative (z 5 20.52). Since the mean of the standard normal distribution is z 5 0,
the z value for any score below the mean will be negative. However, the negative values pose
no problem because all normal distributions are symmetrical, so the proportion of a normal
population between z 5 20.52 and the mean will be the same as that between z 5 0.52 and
the mean. We simply look up the proportion for the appropriate value of z, remembering that
when z is negative, it is a proportion to the left of the mean rather than to the right.
To state all this as a principle, because normal distributions are symmetrical, z scores with the
same absolute value (the same numbers without regard to the sign) include the same proportions between their values and the mean of the distribution. For this reason, the z table indicates only the proportions for half the distribution. In the case of Table 3.2, that half is the
positive (right) half of the distribution.
Try It!: #2
Table 3.2 has table values only for positive
z scores. How do we interpret the value
when z turns out to be negative?
Because 50% of the distribution occurs either side
of the mean, if 19.85% of the distribution is from a
z 5 20.52 back to the mean, the balance of the left
(negative) half of the distribution must occur below
a z score of 20.52. That proportion is 50 2 19.85 5
30.15%, as the number line illustrates:
50%
30.15 | 19.85% |
z 5 20.52
0
Working in the other direction: if the question is what percentage of the population will score
11 or lower on the SoWHAT, the answer is 50 2 19.85 5 30.15%.
© 2016 Bridgepoint Education, Inc. All rights reserved. Not for resale or redistribution.
tan82773_03_ch03_061-090.indd 70
3/3/16 9:57 AM
Section 3.2
The Standard Normal Distribution
If instead someone asks what the probability of scoring at or below 11 (30.15%) is, we must
turn the percentage back into a probability: 30.15 / 100 5 0.3015, or p 5 0.3015 of scoring at
or below 11.
Note that the language above is “11 or lower,” and “at
or below.” The characteristics of the normal curve allow
us to determine the percentage between points, but not
at a discrete point. Technically, a particular point has no
width and so no associated percentage.
Try It!: #3
What is the largest possible value for z?
Converting z Scores to Percentage
Now that we have learned how to transform scores from other distributions to fit the z distribution, we will take a further look at how we can convert scores on opposite sides of the mean
and scores with the same sign to percentages.
Two Scores on Opposite Sides of the Mean
If 5 and 25 are the most extreme apathy scores gathered in the sample of SoWHAT scores, we
might ask what percentage of the entire distribution will score between 5 and 25. Because
those were the lowest and highest scores, the answer should be 100%, correct? Remember
that the collected data were a sample:
5, 6, 9, 11, 15, 15, 17, 20, 22, 25
Although everyone in the sample scored between 5 and 25, it is entirely possible, even probable, that someone in the larger population will have a more extreme score. Using the z distribution, we can determine how probable by following these steps:
1. Convert both 5 and 25 into z scores.
2. Determine the table values for both z scores.
3. Turn the table values into percentages.
4. Add the percentages together.
The z score formula is
z5
x2M
s
Allowing that the subscript to each z indicates the raw score and that M 5 14.5 and s 5 6.737
from the sample data produces the following calculations:
z5 5
5 2 14.5
6.737 5 21.410, for which the table value is 0.4207,
z25 5
25 2 14.5
6.737 5 1.559 5 1.56, which has a table value of 0.4406.
which corresponds to a percentage of 42.07% (0.4207 3 100).
Expressed as a percentage, the value is 44.06% (0.4406 3 100).
© 2016 Bridgepoint Education, Inc. All rights reserved. Not for resale or redistribution.
tan82773_03_ch03_061-090.indd 71
3/3/16 9:57 AM
Section 3.2
The Standard Normal Distribution
Adding the two percentages together to determine the total percentage between them produces the following:
42.07 1 44.06 5 86.13% from 5 to 25.
Clearly, these scores do not equal 100%. The results indicate that in the population for which
these data are a sample, about 13.87% (100 2 86.13) will score either lower than 5 or higher
than 25. Figure 3.4 indicates this result.
Figure 3.4: Areas under the normal curve below z 5 21.41 and beyond z = 1.56
In this distribution, z values that fall below 21.41 or above 11.56 (raw scores below 5 or above 25)
are considered extreme scores, comprising only about 13.87% of the population.
z values: –3z
–2z
–1z
–1.41
0
+1z
+2z
+3z
1.56
About 42% About 44%
The answer to this problem underscores two important concepts. First, remember that we
are dealing with sample data, and the sample will never exactly duplicate a population. The
second, more subtle point reveals that there is no point at which we can be confident that no
one will produce a more extreme score. The curve represents this fact by extending the tails
(the endpoints of the curve) outward in either direction along the horizontal axis. Although
the gap between tail and axis narrows constantly, the tails never touch the axis (the 50-cent
word is that the tails are “asymptotic” to the horizontal axis). The application means a value
of z will never account for 100% of the distribution.
z Scores with the Same Sign
The previous example raised the question about the percentage of the distribution between
z scores on opposite sides of the mean—two z scores where one was positive (z 5 1.56) and
the other negative (z 5 21.41). Perhaps the researcher has a question about the percentage
of the distribution between SoWHAT scores of 15 and 20. When M 5 14.5, both of these raw
scores are higher than the mean and both will result in positive z values. When two z scores
have the same sign, determining the percentage of the distribution between them requires
that we complete the following steps:
© 2016 Bridgepoint Education, Inc. All rights reserved. Not for resale or redistribution.
tan82773_03_ch03_061-090.indd 72
3/3/16 9:58 AM
Section 3.2
The Standard Normal Distribution
1. Calculate z scores for the raw scores.
2. Determine the table values for each z.
3. Subtract the smaller proportion from the larger.
4. Convert the result into a percentage by multiplying by 100.
z5
x2M
s
z15 5
15 2 14.5
6.737 5 0.0742, or 0.07, for which the table value is 0.0279.
The 0.0279 is the proportion of the distribution from z 5 0.07 and the mean of the distribution. For a raw score of 20,
z20 5
20 2 14.5
6.737 5 0.8164, or 0.82, which corresponds to p 5 0.2939.
This is the proportion of the distribution between z 5 0.82 and the mean of the distribution.
When the z scores are on opposite sides of the mean, as they were in our first example, determining the proportion of the distribution between them was a simple matter of adding the two
table values. When both z scores are on the same side of the distribution, however, their table
values overlap. To determine the proportion between two values of z with the same sign, take
the proportion between the larger (absolute) value and the mean minus the proportion from the
smaller (absolute) value to the mean: 0.2939 2 0.0279 5 0.2660. Multiplying that by 100 produces the percentage: 100 3 0.2660 5 26.6% of the distribution will score between 15 and 20.
Figure 3.5 illustrates this result.
Figure 3.5: Areas under the curve between z = 0.07 and z = 0.82
The percentage of scores between two z values with the same sign is determined by calculating the
difference between the smaller z score table value and the larger one, then multiplying the result by 100.
–3z
–2z
–1z
0
+1z
+2z
+3z
z = 0.07 0.82
26.6%
When trying to answer a question about the percentage of the distribution in a particular
area, drawing a simple diagram like Figure 3.5 helps make the question less abstract.
© 2016 Bridgepoint Education, Inc. All rights reserved. Not for resale or redistribution.
tan82773_03_ch03_061-090.indd 73
3/3/16 9:58 AM
Section 3.2
The Standard Normal Distribution
Apply It!
Attention to Detail
A psychological services company administers a test that measures the respondent’s attention to detail. The company’s clients
are employers in a variety of organizations that require people
with good analytical skills. Respondents who score in the lowest ranges of the scale are indifferent to potentially important
details. Those who score in the highest ranges tend to fixate on
details that may be unimportant to an outcome. Individuals who
meet the qualification on this particular test score in the range
from 3.80 to 4.30. Data for those who have taken the test in the
past indicate that M 5 4.00 and s 5 0.120. For researchers, the
initial question is, “Of those who take the test, what proportion
are rejected because either they are inattentive to important
details or they become focused on the wrong details?” In terms
of the z distribution, the equivalent questions are the following:
gerenme/iStock/Thinkstock
(a) What proportion of those who took the test in the past failed to meet the minimum
qualification for attention to relevant detail? In other words, what proportion scored
lower than 3.80?
(b) What proportion of test-takers scored higher than 4.30?
Regarding question (a), to determine the value of z, the following apply:
x 5 3.80
M 5 4.00
s 5 0.12
Since z 5
x2M
5 (3.80 2 4.00) / 0.120
s
z3.80 5 21.67
The z score table (Table 3.2) indicates that a proportion of 0.4525 of the entire population will
fall between this z score and the mean of the distribution. However, the researchers’ interest is
in the proportion below this point. Therefore,
0.5 2 0.4525 5 0.0475
In other words, a proportion of 0.0475 occurs below x 5 3.80. Stated as a percentage, 4.75%
of the candidates will score below 3.80 on the test.
For the proportion above 4.30,
z4.30 5 (4.30 2 4.00) / 0.12 5 2.5
Table 3.2 indicates that
• this z score corresponds to a proportion of 0.4938, indicating that, as a percentage,
49.38% of the population occurs between a score of 4.30 and the mean of the distribution, and
• the percentage above this point will be 50 2 49.38 5 0.62, or 0.62%, of those who take
the test score at 4.30 or beyond.
Apply It! boxes written by Shawn Murphy
© 2016 Bridgepoint Education, Inc. All rights reserved. Not for resale or redistribution.
tan82773_03_ch03_061-090.indd 74
3/3/16 9:58 AM
Section 3.2
The Standard Normal Distribution
Comparing Data from Different Tests
Earlier chapters discussed how test scores from two different instruments with different
means and standard deviations can be compared. Perhaps a juvenile gang member under
court-ordered counseling is required to complete two different assessments: one measuring
aggression and one social alienation. The gang member scores 39 on the aggression test and
15 on the alienation test. Table 3.3 shows the means and standard deviations of the two tests.
Table 3.3: Test results for aggression and social alienation
Test
Mean
Standard deviation
Aggression measure
32.554
5.824
Social alienation
12.917
2.674
In both cases, the gang member scored higher than average on both aggression and social
alienation. For which measure is the score the most extreme?
Because the two tests have different means and standard deviations, comparing the raw
scores directly is not helpful. However, employing the z transformation allows both scores to
fit a distribution where the mean is 0 and the standard deviation is 1.0. The raw scores may
not reveal much, the z scores can be directly compared. Recall that
z5
x2M
s
Calculating z for the aggression score produces:
z39 5
39 2 32.554
5 1.107
5.824
z15 5
15 2 12.917
5 0.779
2.674
Then calculate the z for social alienation:
Interpreting Multiple z Values
Since the question is which of the juvenile’s two test
scores is the more extreme, we have no need for
table values—only the value of z. As both z values are
positive, the z for aggression is more extreme than
that for social alienation. Performing the z transformation allows us to note that the aggression value
is 1.107 standard deviations from the mean of the
distribution. Alienation, meanwhile, is just 0.779
standard deviations from its mean. Practically, the
results show this individual is more aggressive than
alienated. As long as raw scores, means, and standard deviations are available, researchers can use
Doug Menuez/Photodisc/Thinkstock
Using z scores enables researchers
to better understand test results
measuring aggression and social
alienation in juvenile gang members.
© 2016 Bridgepoint Education, Inc. All rights reserved. Not for resale or redistribution.
tan82773_03_ch03_061-090.indd 75
3/3/16 9:59 AM
Section 3.2
The Standard Normal Distribution
z to make direct comparison of very different qualities, in this case, aggression and social
alienation in the same individual.
Another Comparison
Psychologist Lewis Terman developed the Stanford-Binet test, which measures children’s intelligence. Suppose a psychologist is similarly interested in giftedness among children. Because
unusual verbal ability often seems to accompany superior intelligence in gifted children, the
psychologist measures both characteristics for a group of subjects. One particular subject scores
140 on intelligence and 55.0 on verbal ability. Table 3.4 lists the descriptive data for each test.
Table 3.4: Test results for intelligence and verbal ability
Test
Mean
Intelligence
100
Verbal ability measure
Standard deviation
40
15
5.451
As in the previous example, the researcher must convert scores into z scores before they can
be directly compared.
For the intelligence score, the z score is calculated as:
x2M
s
140 2 100
z140 5
5 2.667
15
z5
For the verbal ability measure, the z score is calculated as:
x2M
s
55 2 40
z55 5
5.451
z5
5 2.752
The z scores indicate that both test scores are about the same distance from their respective
means. This makes it more difficult to glance at the raw scores and know which is higher. But
because both have been transformed into z scores, the two measures now belong to a common distribution, and the researcher can see that the verbal ability measure is slightly higher
than the intelligence score.
Determining How Much of the Distribution Occurs
Under Particular Areas of the Curve
If we draw a distribution and clarify what is at issue, questions about how much of the distribution is above a point, below a point, or between two points do not require researchers to
observe formal rules. For the sake of order and clarity, however, the flowchart in Figure 3.6
provides some direction for answering different questions a researcher might ask about proportions within a distribution.
© 2016 Bridgepoint Education, Inc. All rights reserved. Not for resale or redistribution.
tan82773_03_ch03_061-090.indd 76
3/3/16 9:59 AM
Section 3.2
The Standard Normal Distribution
Figure 3.6: Flowchart to address questions pertaining to a distribution
Use the steps illustrated in the flowchart to resolve questions about the proportions within a
population.
Questions about the proportions
of a population
Below a score
Above a score
Determine the
z value
Determine the
z value
Locate the proportion in Table 3.2
Locate the proportion in Table 3.2
Negative z?
Subtract the
table value
from 0.50
Positive z?
Add the table
value to 0.50
Positive z?
Subtract the
table value
from 0.50
Between two scores
Negative z?
Add the table
value to 0.50
Above and below two scores
Scores on opposite
sides of the mean
Scores on the same
side of the mean
Scores on opposite
sides of M
Scores on same
side of M
Calculate both
zs and locate
table values
Calculate both
zs and locate
table values
Calculate both zs
and locate
table values
Calculate both zs
and locate
table values
Sum the
table values
Subtract the smaller
value from the larger
Subtract both values
from .050 and sum
Subtract the smaller
value from the larger
and subtract the
result from 1.0
The list of steps must seem like a great deal to remember. In fact, the better course when confronted with a
z score problem is to sketch out a distribution to produce something like Figures 3.3 and 3.4. The visual
displays help clarify the question and suggest the steps
needed to answer it.
Try It!: #4
Figuratively speaking, how does the z
transformation allow you to compare
apples to oranges?
© 2016 Bridgepoint Education, Inc. All rights reserved. Not for resale or redistribution.
tan82773_03_ch03_061-090.indd 77
3/3/16 9:59 AM
Section 3.3
z Scores, Percentile Ranks, and Other Standard Scores
3.3 z Scores, Percentile Ranks, and Other Standard Scores
Our task to this point has been to transform raw scores into z scores and then to percentages or proportions of the distribution in specified areas. If the percentages are already available, but neither the raw data nor the related descriptive statistics are, Table 3.2 (the z table)
allows us to work backward to determine the z value—even without the mean and standard
deviation for the data.
Let us assume that published data indicate that only 1% of the population has intelligence
scores above 140. What z score does this represent?
1. Because Table 3.2 lists proportions, the first step is to turn the percentage into a
proportion: 1% is 1/100, which is the same as a proportion of 0.01.
2. Recall that Table 3.2 indicates the proportion of a normal population between a
particular value of z and the mean for half (0.5) of the distribution. Therefore, we
need a z value which includes all but that most extreme 0.01, which will be the
z value for a proportion of 0.50 2 0.01 5 0.49. A z value for a proportion of 0.49,
will be the value that includes the 49% of the distribution, which means it excludes
the highest 1% of the distribution.
3. Table 3.2 does not list a proportion of exactly 0.49, but it does list 0.4901, which
is very close. Reading leftward from the proportion to the margin and also
vertically to the column heading, the associated z value for 0.4901 is 2.33. If data
were gathered for intelligence scores, a z 5 2.33 excludes close to the top 0.01
or 1%.
To state this more directly, when viewed as z scores, any intelligence score where z . 2.33
is somewhere among the top 1% of all intelligence scores. Figure 3.7 illustrates this
proportion.
Figure 3.7: The value of z associated with a particular proportion
A normal distribution curve that shows where the highest 1% of scores fall within a given population.
–3z
–2z
–1z
0
+1z
+2z
+3z
z = 2.33
proportion = 0.01
© 2016 Bridgepoint Education, Inc. All rights reserved. Not for resale or redistribution.
tan82773_03_ch03_061-090.indd 78
3/3/16 9:59 AM
Section 3.3
z Scores, Percentile Ranks, and Other Standard Scores
Converting z Scores to Percentile Ranks
Chapter 2 introduced percentile scores. Recall that percentiles indicate the point below
which a specified percentage of the group occurs. For example, 73% of the distribution occurs
at or below the point defined by the 73rd percentile, and so on. Because researchers can
use the table values associated with z scores to determine the percentage of the distribution
occurring below a point, it is not difficult to take one more step and turn that percentage into
a percentile score. For example, because
• z 5 1.0 includes 34.13% between that point and the mean and
• that part of the distribution from the mean downward is 50%, then
• 34.13% 1 50% 5 84.13% of scores are at or below z 5 1.0; therefore, z 5 1.0 occurs
at the 84th percentile.
Although percentile scores can be easily determined from the table values that are associated with z scores, note an important difference between percentile scores and z scores. The
z score is one of several standard scores. Standard scores are all equal-interval scores—the
interval between consecutive integers is constant, which means that in terms of data scale,
standard scores are interval scale. The increase in whatever is measured from z 5 21.5 to
z 5 21.0 is the same as it is from z 5 0.3 to z 5 0.8. The increase is 0.5 in either case.
This interval scale does not apply to percentile scores. Because these scores indicate the percentage of scores below a point rather than reflecting a direct measure of some characteristic,
the distances between consecutive scores differ widely in various parts of the distribution.
Most of the data in any normal distribution are in the middle portion, where scores have the
greatest frequency. The frequency with which scores occur diminishes as scores become
more distant from the mean, something reflected in the curves in frequency distributions that
are vertically highest in the middle and then decline as they extend outward to the two tails.
Note the comparison between percentiles and z scores in Figure 3.8.
Figure 3.8: z scores and percentile scores
A comparison of z scores and percentiles for a normal distribution shows that the majority of scores
are found within the 50th percentile. Meanwhile, the frequency of scores above the 99th and below
the 1st percentiles is low in a normal distribution.
z scores
Percentiles
–3
–2
–1
0
+1
+2
+3
99th
© 2016 Bridgepoint Education, Inc. All rights reserved. Not for resale or redistribution.
tan82773_03_ch03_061-090.indd 79
3/3/16 9:59 AM
Section 3.3
z Scores, Percentile Ranks, and Other Standard Scores
As a result of high frequency in the middle of the distribution, in any normal distribution the
difference between consecutive percentile scores is always much smaller near the middle of
the distribution (between the 50th and 51st percentiles, for example) than between consecutive percentile scores in the tails (between the 10th and 11th, or the 90th and 91st percentiles, for example). This characteristic has important implications. The difference between
scoring at the 50th and 51st percentile score on something like the Beck Depression Inventory is almost inconsequential compared to the difference between the 90th and 91st percentile, a much greater difference. Percentile scores are ordinal scale, whereas z scores are
interval scale.
Converting z to Other Standard Scores
Part of the appeal of the z score is that it enables researchers to readily determine relative performance. A positive z value indicates that the individual has scored in the upper
half of the distribution. Someone who scores one standard deviation beyond the mean, as
we noted earlier, has scored at the 84th percentile, and so on. The z scores belong to a
family of measures called “standard scores.” They have in common these characteristics:
a) a fixed mean and standard deviation and b) equal intervals between consecutive data
points.
Another standard score is the t score. It is used in the place of z scores when those reporting
them prefer not to report negative scores, which of course are half of all possible z values.
After calculating the z value, a researcher can easily change it to a t score. In fact this is true
for any score that has a fixed mean and standard deviation, whether it is a standard score like
t or, for example, a Graduate Record Exam (GRE) score (see Table 3.5), which also has a fixed
mean and standard deviation.
Table 3.5: Comparison of t scores and GRE scores
t scores
Graduate Record Exam
Mean
Standard deviation
50
10
500
100
Either score can be derived from z. To convert from z to t, for example, simply multiply z by 10
and add 50. So, if z 5 1.75, then
t 5 10 3 1.75 5 17.5 1 50 5 67.5
z 5 1.75 is the same as t 5 67.5.
For GRE, we would multiply z by 100 and add 500:
GRE 5 100 3 1.75 5 175.0 1 500 5 675
z 5 1.75 is the same as GRE5 675 (and as t 5 67.5).
© 2016 Bridgepoint Education, Inc. All rights reserved. Not for resale or redistribution.
tan82773_03_ch03_061-090.indd 80
3/3/16 9:59 AM
Section 3.4
Using Excel to Perform the z Score Transformation
Although more common in educational than in psychological testing and research, normal curve equivalent
scores (NCE) and “stanine” scores (standard nine-point
scale) are also examples of standard scores. Like z and
t, each is equal-interval, and both have fixed means and
standard deviations.
Try It!: #5
What makes a score a standard score?
3.4 Using Excel to Perform the z Score Transformation
The z score transformation is a fairly simple formula. As a result, to program it into Excel and transform an entire data set into z scores is not difficult.
In fact, the application offers several ways to do this,
but this chapter will explore just one. It involves
programming the z score transformation formula
directly into the data sheet.
A researcher interested in the relationship between
poverty and achievement motivation among
secondary-school-aged young people gathers data
from a group of students whose families qualify
for free and reduced-price lunches at school. The
achievement motivation scores are as follows:
4, 5, 7, 7, 8, 9, 9, 9, 10, 13
monkeybusinessimages/iStock/Thinkstock
Evaluating achievement motivation
scores can give researchers valuable
information about the relationship
between poverty and achievement in
schools.
To use Excel to transform those data into their z score equivalents, follow these steps:
1. List the data in Excel in Column B, with the label “Ach Mot” in B1.
2. Enter the 10 scores into cells B2 to B11.
3. In cell B12, enter the formula =average(B2:B11). (Note: Virtually all spreadsheets,
including Excel, have shortcuts for the more common calculations, such as means
and standard deviations. A user can enter the formula, as we have done here, or use
a shortcut. Shortcut procedures vary, however, depending on the operating system
and the version of Excel. Excel for Mac, for example, allows users to enter the data,
position the cursor where they desire the statistic’s value to appear, and then double-click the name of the desired statistic under the Formula tab.)
a. The equal sign indicates to Excel that a formula follows.
b. The command average will provide the arithmetic mean.
c. When several cells are to be included in the function, they are placed in paren
theses ( ). When the cells are consecutive, the colon (:) indicates that all cells
from B2 to B11 are to be included in the function.
4. Press Enter.
5. In cell A12, enter the label “mean 5.” The value in cell B12 will be 8.1, the mean of
the achievement motivation scores.
© 2016 Bridgepoint Education, Inc. All rights reserved. Not for resale or redistribution.
tan82773_03_ch03_061-090.indd 81
3/3/16 9:59 AM
Using Excel to Perform the z Score Transformation
Section 3.4
6. In cell B13, enter the formula =stdev(B2:B11). Note that stdev is the Excel
abbreviation for “sample standard deviation.” For Mac users, the abbreviation is
stdev.s.
7. Press Enter.
8. In cell A13, enter the label std dev =. The value in cell B13 will be 2.558211, the
standard deviation of the scores.
9. In cell C1, enter the label equiv z.
10. In cell C2, enter the formula =(B2_8.1)/2.558 and press Enter. Consistent with the
z score transformation, this formula subtracts the mean from the raw score in cell
B2 and then divides the result by the standard deviation, 2.558, which we rounded
to three decimals.
11. Repeat that operation for all the other scores as shown next:
a. With the cursor in cell C2, click and drag the cursor down from C2 to C11 so that
cells C2 to C11 are highlighted.
b. In the Editing section at the top of the page near the right side is a Fill command
with a down-arrow at the left (for Macs, the command is on the left side, below
the Home tab). Click the down-arrow to the right of the Fill command, then click
Down. This action will repeat the result in C2 for the other nine cells, adjusting
for the different test scores in each cell.
Figure 3.9 shows how the spreadsheet will look after Step 11, with the z score equivalents
of all the original achievement motivation scores displayed to the right of the original
scores.
Figure 3.9: Raw scores transformed to z scores in Excel
Excel converts raw scores to z scores using a simple formula.
Source: Microsoft Excel. Used with permission from Microsoft.
© 2016 Bridgepoint Education, Inc. All rights reserved. Not for resale or redistribution.
tan82773_03_ch03_061-090.indd 82
3/3/16 9:59 AM
Using z Scores to Determine Other Measures
Section 3.5
3.5 Using z Scores to Determine Other Measures
Occasionally, a researcher has access to z scores and the mean and standard deviation
but not the original raw scores. Formula 3.1 used the raw score (x), the mean (M), and
the standard deviation (s) to determine the value of z, but actually, any three of the values in the formula can be used to determine the value of the fourth. Just as Formula 3.1
uses x, M, and s to determine z, we could use z, M, and s to derive x. Altering Formula
3.1 to determine the value of something other than z involves a little algebra but is not
difficult.
Determining the Raw Score
To determine the raw score, follow these steps:
1. Because z 5 (x 2 M)/s, swap the terms before and after the equal sign so that
(x 2 M)/s 5 z.
2. To eliminate the s in the denominator of the first term, multiply both sides
by s so that it disappears from the first term and emerges in the second:
x 2 M 5 sz.
3. To isolate x, add M to both sides of the equation so that x 5 sz 1 M.
Returning to the Excel problem, if the z scores and descriptive statistics are available, we can
determine the raw score for which z 5 21.603 as follows:
If M 5 8.10, s 5 2.558, and x 5 z 3 s 1 M, substituting the values we have
produces x 5 (21.603)(2.558) 1 8.10 5 3.9995, which rounds to 4.0.
Checking the earlier data reveals that 4 was indeed the raw score for which z 5 21.603.
Determining the Standard Deviation
If the raw scores, the mean, and z are available, but s is lacking, z 5 (x 2 M)/s, so (x 2 M)/s 5 z.
Taking the reciprocal of each half of the equation—which means inverting the term so that
(x 2 M)/s becomes s/(x 2 M) and z/1 becomes 1/z, giving us s/(x 2 M) 5 1/z. Multiplying
both sides by (x 2 M) yields s 5 (x 2 M).
Using the data from the Excel problem again, for the first participant, x 5 4, M 5 8.10, and
z 5 21.603. According to the adjusted formula,
s 5 (x 2 M)/z
therefore, substituting the values we have produces the following:
s5
4 2 8.1
5 2.5577
21.603
which rounds to 2.558, the standard deviation value for the original data set.
© 2016 Bridgepoint Education, Inc. All rights reserved. Not for resale or redistribution.
tan82773_03_ch03_061-090.indd 83
3/3/16 9:59 AM
Using z Scores to Determine Other Measures
Section 3.5
Determining the Mean
It would be very unusual for a researcher to have the z scores, the standard deviation, and the
original achievement motivation score but not have the mean. However, just to complete the
set, the mean can be determined from the other three values as follows:
Because
z 5 (x 2 M)/s
if both halves of the equation are multiplied by s, then s appears in the first
term and disappears from the second. The result is
sz 5 x 2 M
If M is then added to both sides, M appears in the first term and is eliminated
in the second. The result is
sz 1 M 5 x.
If sz is then subtracted from both sides, it is eliminated from the first term and
added to the second. The result is
M 5 x 2 sz
For the first participant, the achievement motivation score x 5 4.0, the z score
5 21.603, and s 5 2.558. The mean for the test can be determined as follows:
M 5 x 2 sz, or
M 5 4 2 (2.558 3 21.603) 5 8.10, which was the original mean.
Maintaining Fixed Means and Standard Deviation
One of the characteristics of widely used standardized tests is that their mean and standard deviation values remain the same over time. The major intelligence tests, for example, have a fixed mean
of 100 and a standard deviation of 15, even though the Stanford-Binet and Wechsler tests have
been revised several times. When a test is revised and updated, do the means and standard deviations likewise change? In fact, they do. Flynn and Weiss (2007) documented significant increases
in intelligence scores over a 70-year period, but to make the scores comparable over time, psychologists use what are called modified standard scores. The modified standard score allows
those working with the test to gather data that have any mean and any standard deviation and
then adjust them so that they conform to predetermined values. This process follows these steps:
1. Gather data with the new instrument.
2. Determine the equivalent z scores for test-takers’ raw scores.
3. Apply the formula.
© 2016 Bridgepoint Education, Inc. All rights reserved. Not for resale or redistribution.
tan82773_03_ch03_061-090.indd 84
3/3/16 9:59 AM
Using z Scores to Determine Other Measures
Section 3.5
Formula 3.2 is used to modify a score so that the mean and standard deviation for the population of scores take on specified values.
Formula 3.2
MSS 5 (sspec)(z)1 Mspec
where
MSS 5 the modified standard score,
sspec 5 the specified standard deviation, and
Mspec 5 the specified mean.
Note that this formula is the same used to transform z scores into t scores. By way of an
example, perhaps a psychologist has developed what she has labeled the Brief Intelligence
Test (BIT). To compare results to tests her colleagues have used traditionally, she wants the
BIT’s descriptive characteristics to conform to those of the more established tests. For eight
participants, the BIT scores are as follows:
22, 25, 26, 29, 29, 32, 32, 35
Of course, no one norms an intelligence test on only eight people. The potential for what we
will later call sampling error is too great. Still, to illustrate the process, we will assume the
sample scores are valid.
Verify that M 5 28.75 and s 5 4.268.
For the participant with an intelligence score of 22, the corresponding z value is
z5
x2M
22 2 28.75
5
5 21.582
s
4.268
To determine that participant’s score on an instrument with a mean of 100 and a standard
deviation of 15, the psychologist will apply the formula:
MSS 5 (sspec)(z) 1 Mspec
5 (15)(51.582) 1 100
5 76.276
Although the original BIT score was 22, using the z transformation and modified standard
score procedures makes the BIT score conform to the mean and standard deviation of a more
established test. Among scores for which the mean is 100 and the standard deviation is 15,
the modified standard score for the BIT score of 22 is 76.276.
© 2016 Bridgepoint Education, Inc. All rights reserved. Not for resale or redistribution.
tan82773_03_ch03_061-090.indd 85
3/3/16 9:59 AM
Summary and Resources
Writing Up Statistics
Although z scores are an important part of data analysis, like the raw scores that researchers
gather in their work, z scores often do not appear in research reports. Reports list the means
and standard deviations, but often omit the raw scores and their z score transformation. In
a study of the weight-gain side effect that anti-psychotic drugs might have on adolescents,
Overbeek (2012), however, used a combination of height and weight to determine bodymass-index (BMI) scores for each subject, and then transformed the BMI scores into easierto-interpret z scores. A z score near 0 indicated that given the subject’s height, weight was
probably appropriate. A positive z score indicated that the individual might be overweight,
negative z scores indicated underweight, and so on. Overbeek also used z scores to index the
weight-gain data over the course of the study.
Brown (2012), too, used z scores. In his study, they offered a way to counter the effect that
grade inflation has on college students’ class rankings. He posited that class rankings are less
informative than they once were because weaker students in departments where coursework
is easier are ranked ahead of students who have a higher level of academic aptitude but compete in more demanding programs. Brown’s solution was to use the z transformation within
departments to indicate how much above or below the mean students were in their individual programs.
Summary and Resources
Chapter Summary
Normal distributions are unimodal and symmetrical, and their standard deviations tend
to be about one-sixth of the range. Although not all data are normally distributed, many
of the mental characteristics that psychologists and social scientists measure are normal.
Because the proportions of the population that occur in specified ranges remains constant
in normally distributed populations, we can have some confidence about how scores will be
arrayed even before we view a display of the data.
What the standard normal distribution, or z distribution, does is capitalize on the consistency in normally distributed populations by offering one distribution by which all other
normal populations can be referenced. In this distribution, where the mean is always 0 and
the standard deviation is 1.0 (Objective 1), table values indicate the proportions of the population likely to occur anywhere along its range. By transforming raw scores (Objective 2)
from any normal population so that they fit this z distribution, we can take advantage of
how well the characteristics of this distribution are known and answer important questions
about data from any population (Objective 3) in terms of z:
•
•
For example, when someone scores at a particular level, we can ask what proportion
of the entire population is likely to score below (or above) that point.
When most of the people in a particular group score between two points, we can ask
what proportion of the entire population will score between (or outside) those points.
Because the z score transformation is a relatively simple formula, programming Excel to
produce the z equivalents for any set of scores (Objective 4) is simple and can be helpful
with large data sets.
© 2016 Bridgepoint Education, Inc. All rights reserved. Not for resale or redistribution.
tan82773_03_ch03_061-090.indd 86
3/3/16 9:59 AM
Summary and Resources
The z is one of several standard scores in fairly common use. Whether z or some other, all
standard scores indicate how distant one individual’s score is from the mean of the distribution. Rather than providing an absolute measure of some characteristic, standard scores are
normative, meaning that they indicate the level of what is measured relative to others in the
same population. Those who prefer not to deal in negative values (which characterize half of
the z distribution) can employ t scores. In all material respects, t is the same as z, except that
the mean is 50 and the standard deviation is 10.
The modified standard score (Objective 6) enhances standard scores’ ability to communicate an individual’s standing relative to a population. Researchers often use standard scores
to report the data from standardized tests, but these tests are revised from time to time,
which can affect the test means and standard deviations. To ensure stability, the modified
standard score uses the z transformation as a way to maintain constant descriptive characteristics, even as the instrument used to measure it, or even the characteristic measured,
changes with time.
In the incremental nature of statistics books, each chapter prefaces the next. Chapters 1–3
are a prelude to Chapter 4. With all our effort to label, display, and describe data sets, the
focus in the discussion of z scores and the other topics has been primarily about analyzing
the performance of individuals. Behavioral scientists, however, are generally much more
interested in asking questions about groups. Analyzing how those in a sample compare to
those in the entire population is the focus of Chapter 4. It will do so by expanding discussion
of the z distribution.
The math and the logic involved in Chapter 4 will be much the same. If the discussion in this
chapter makes sense, the material in Chapter 4 will not be difficult. Still, it is a good idea to
review the Chapter 3 material and recalculate the sample problems, as repetition has value.
Key Terms
modified standard scores Standard scores
adjusted to reflect a specified mean and
standard deviation.
standard scores Normally distributed,
equal-interval scores that have a fixed mean
and standard deviation.
probability The measure of the likelihood
that an event will occur. The values range
from p 5 0, for events that never occur,
to p 5 1.0, for events that occur every
time.
z score The score that results when scores
from any source are made to conform to the
characteristics of the standard normal, or z,
distribution. The z distribution has M 5 0
and s 5 1.
percentile A value below which a certain
percentage of all scores in a distribution may
be found; 37% of all scores occur below the
37th percentile.
standard normal distribution A normal
distribution in which µ 5 0 and s 5 1.0.
t score A standard score based on a normal
distribution in which M 5 50 and s 5 10.
They are sometimes preferred to z scores
because they rarely involve negative values.
z transformation Changes any raw score
into a z score so that it fits the standard
normal distribution.
© 2016 Bridgepoint Education, Inc. All rights reserved. Not for resale or redistribution.
tan82773_03_ch03_061-090.indd 87
3/3/16 9:59 AM
Summary and Resources
Review Questions
Answers to the odd-numbered questions are provided in Appendix A.
1. A researcher is interested in people’s resistance to change. For the dogmatism scale
(DS), data for 10 participants are as follows:
28, 28, 29, 29, 32, 33, 35, 36, 39, 42
a. What is the z score for someone who has a DS score of 28?
b. Will a z score for a raw score of 35 be positive or negative? How do you know?
c. How many standard deviations is a score of 28 from the mean?
d. What will be the z value of a raw score of 33.1?
e. Since there are no scores below 28, does it make any sense to calculate z for
a raw score of 25, for example? Shouldn’t such a score have a zero probability
of occurring?
2. Examining the relationship between recreational activity and level of optimism
among senior citizens, a psychologist develops the Recreation Activity Test (RAT).
Scores for 8 participants are as follows:
11, 11, 14, 14, 14, 17, 18, 22
a. What is the z score for someone with RAT 5 23?
b. Why isn’t 0 the answer to 2a, since none of the participants scored 23?
c. What is the z score for someone with RAT 5 15.125?
d. Explain the answer to 2c.
e. How does z allow one to compare tests with entirely different means and standard
deviations?
3. One participant has RAT 5 11. The same individual is administered a Consistent
Approval Test (CAT) and scores 45. The CAT data, including that participant’s score,
are as follows:
42, 45, 48, 49, 55, 58, 62, 64
a. Which score is higher, the RAT or the CAT?
b. Why isn’t the answer to 3a automatically CAT, since it has the higher mean value?
4. Researchers developed the ANxious, Gnawing Stress Test (ANGST) to measure
emotional stability among law-enforcement professionals. A random sample of
police patrol officers yielded the following scores:
54, 58, 61, 64, 75, 81, 82, 85
a. What proportion of the population will score 81 or higher?
b. What proportion will score 60 or higher?
c. If x . 75 is the cutoff for “highly stressed,” what is the probability that someone,
selected at random, will be highly stressed?
d. What is the probability of scoring between 60 and 81?
© 2016 Bridgepoint Education, Inc. All rights reserved. Not for resale or redistribution.
tan82773_03_ch03_061-090.indd 88
3/3/16 9:59 AM
Summary and Resources
5. Using the data in Question 4, what percentage of the population will score lower
than 55?
6. What is the t equivalent to a z score for someone with an ANGST score of 64?
a. What is the mean of the t distribution?
b. Why is t sometimes preferred over z?
c. If z 5 2.5, what is t?
7. Refer to the data in Questions 3 and 4: For an individual who scores 60 on RAT and
78 on ANGST, which is the higher score?
8. In any standard normal distribution, determine the following:
a. What percentage of scores will occur below z 5 0?
b. What is the probability of a positive value of z?
c. What percentage of scores will occur between ±1.96 z?
9. If someone scores z 5 1.0, what is the corresponding percentile rank?
10. What percentile rank is z 5 0? What measure of central tendency represents the
50th percentile?
11. A psychologist wishes to maintain a mean of 25 and a standard deviation of 5 for
a test developed to measure compulsive behavior. On a revised test, the scores are
as follows:
14, 17, 19, 19, 22, 27, 28, 29
a. What is the modified standard score for the person who scored 17 on the revised
instrument?
b. What is the probability of scoring 17 or lower according to the eight scores?
12. Given the data in Question 11,
a. What is the z equivalent of a raw score of 28?
b. What is the probability of scoring somewhere from 14 to 29?
13. Draw a normal distribution and identify where z 5 21.17 and z 5 12.53 are
located. What percentage of the population occurs between these two z values?
Answers to Try It! Questions
1. A z of 1.5 indicates that the associated raw score is 1.5 standard deviations (the
denominator in z) from the mean.
2. Because the standard normal distribution (the z distribution) is normal, the distribution is symmetrical. The proportion of the distribution between a value of z and
© 2016 Bridgepoint Education, Inc. All rights reserved. Not for resale or redistribution.
tan82773_03_ch03_061-090.indd 89
3/3/16 9:59 AM
Summary and Resources
the mean will be the same for a negative z as it is for a positive z with the same
numerical value.
3. Do not refer to Table 3.2 for help with this one. The table’s highest score is z 5 3.09,
but in fact z has no upper limit. In theory, the tails in the z distribution never actually
touch the horizontal axis of the graph, which means that there exists always at least
the possibility of scores higher (or lower) than any already measured.
4. One of the values of the z transformation is that scores that have any descriptive
characteristics can be recalibrated so that they fit a distribution where the mean is 0
and the standard deviation is 1.0. By doing so, scores from any variety of sources can
be compared directly after converting them to z scores. The only requirement is that
they be normally distributed.
5. Standard scores are equal-interval scores with a fixed mean and standard deviation,
thereby allowing the magnitude of the score to indicate how an individual compares
to all others for whom scores are available.
© 2016 Bridgepoint Education, Inc. All rights reserved. Not for resale or redistribution.
tan82773_03_ch03_061-090.indd 90
3/3/16 9:59 AM
Applying z to Groups
4
Victor Faile/Corbis
Chapter Learning Objectives:
After reading this chapter, you should be able to do the following:
1. Describe the distribution of sample means.
2. Explain the central limit theorem.
3. Analyze the relationship between sample size and confidence in normality.
4. Calculate and explain z test results.
5. Explain statistical significance.
6. Calculate and explain confidence intervals.
7. Explain how decision errors can affect statistical analysis.
8. Calculate the z test using Excel.
91
© 2016 Bridgepoint Education, Inc. All rights reserved. Not for resale or redistribution.
tan82773_04_ch04_091-120.indd 91
3/3/16 2:30 PM
Section 4.1
Distribution of Sample Means
Introduction
As we noted at the end of Chapter 3, researchers are generally more interested in groups
than in individuals. Individuals can be highly variable, and what occurs with one is not
necessarily a good indicator of what to expect from someone else. What occurs in groups,
on the other hand, can be very helpful in understanding the nature of the entire population. A Google search indicates that the suicide rate is higher among dentists than it is
among those of many other professions. If we wanted to experiment with some therapy
designed to relieve depressive symptoms among dentists, we would be more confident
observing how a group of 50 dentists responds than in examining results from just one.
This chapter will use the material from the first three chapters to begin analyzing people
in groups.
Noting that many of the characteristics that interest behavioral scientists are normally distributed in a population implies that some characteristics are not. Since samples can never
exactly emulate their populations, it may not be clear in the midst of a particular study
when data are normally distributed. This uncertainty potentially poses a problem: we may
wish to use the z transformation and Table B.1 of Appendix B in our analysis, but Table B.1
is based on the normality assumption. If the data are not normal, where does that leave the
related analysis?
4.1 Distribution of Sample Means
What options do researchers have if they are suspicious about data normality? One important answer
is the distribution of sample means, so named
because the scores that constitute the distribution
are the means of samples rather than individual
scores.
Note that the descriptor population means all possible members of a defined group. Recall that the
frequency distribution—the bell-shaped curve representing the population—was a figure based on
the individual measures sampled one subject at a
time. In discussing the frequency distribution, we
assumed that we would measure each individual
on some trait, and then plot each individual score.
Instead of selecting each individual in a population
one at a time, suppose a researcher
1. selects a group with a specified size;
2. calculates the sample mean (M) for each
group;
3. plots the value of M (rather than the value
of each score) in a frequency distribution;
4. and continues doing this until the population is exhausted.
iStockphoto/Thinkstock
A population is all members of a
defined group, such as all voters in a
county.
© 2016 Bridgepoint Education, Inc. All rights reserved. Not for resale or redistribution.
tan82773_04_ch04_091-120.indd 92
3/3/16 2:30 PM
Distribution of Sample Means
Section 4.1
How would plotting group scores rather than individual ones affect the distribution? Would
the end result still be a population? The answer to the second question is yes: because every
member is included, it is still a population. Whether a population is measured individually or
as members of a group is incidental, as long as all are included.
Perhaps researchers are interested in language development among young children and wish to
measure mean length of utterance (MLU) in a county population. Whether the researchers measure and plot MLU for each child in a county’s Head Start program or plot the mean MLU for every
group of 25 in the program, the result is population data for Head Start learners for that county.
The Central Limit Theorem
The answer to the question “how would the distribution be affected?” is a little more involved,
but it is important to nearly everything we do in statistical analysis. It involves what is called
the central limit theorem:
If a population is sampled an infinite number of times using sample size n and
the mean (M) of each sample is determined, then the multiple M measures
will take on the characteristics of a normal distribution, whether or not the
original population of individuals is normal.
Take a minute to absorb this. A population of an infinite number of sample means drawn from
one population will reflect a normal distribution whatever the nature of the original distribution. A healthy skepticism prompts at least two questions: 1) How would we prove whether
this is true since no one can gather an infinite number of samples? and 2) Why does sampling
in groups rather than as individuals affect normality?
Although prove is too strong a word, we can at least provide evidence for the effect of the
central limit theorem using an example. Perhaps a psychologist is working with 10 people
on their resistance to change, their level of dogmatism. Technically, because 10 constitutes
the entire group, the population is N 5 10. Recall that N refers to the number in a population.
Even with a small population we cannot have an infinite number of samples, of course, but for
the sake of the illustration we will assume that
• dogmatism scores are available for each of the 10 people;
• the data are interval scale;
• the scores range from 1 to 10; and
• each person receives a different score.
So with N 5 10, the scores are 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. Figure 4.1 depicts a frequency distribution of those 10 scores.
The distribution in Figure 4.1 is not normal. With R 5 10 21 5 9 and s 5 3.028 (a calculation
worth checking), the distribution is extremely platykurtic (i.e., flatter than normal); the range
is less than 3 times the value of the standard deviation rather than the approximately 6 times
associated with normal distributions. There is either no mode or there are 10 modes, neither
of which suggests normality. We can illustrate the workings of the central limit theorem with
a procedure Diekhoff (1992) used. We will use samples of n 5 2, and make the example manageable by using one sample for each possible combination of scores in samples of n 5 2 from
the population, rather than an infinite number of samples.
© 2016 Bridgepoint Education, Inc. All rights reserved. Not for resale or redistribution.
tan82773_04_ch04_091-120.indd 93
3/3/16 2:30 PM
Section 4.1
Distribution of Sample Means
Figure 4.1: A frequency distribution for the scores 1 through 10: Each score
occurring once
A frequency distribution of ten scores, each with a different value. This type of distribution, which is
not normal, is highly platykurtic.
10
Score Frequency
9
8
7
6
5
4
3
2
1
1
2
3
4
5
6
7
8
9
10
Score Values
Table 4.1 lists all the possible combinations of two scores from values 1–10. Ninety combinations of the 10 dogmatism scores are possible. The larger the sample size, the more readily
it demonstrates the tendency toward normality, but all combinations of (for example) three
scores would result in a very large table.
Table 4.1: All possible combinations of the integers 1–10
1, 2
1, 3
1, 4
1, 5
1, 6
1, 7
1, 8
1, 9
1, 10
2, 1
2, 3
2, 4
2, 5
2, 6
2, 7
2, 8
2, 9
2, 10
3, 1
3, 2
3, 4
3, 5
3, 6
3, 7
3, 8
3, 9
3, 10
4, 1
4, 2
4, 3
4, 5
4, 6
4, 7
4, 8
4, 9
4, 10
5, 1
5, 2
5, 3
5, 4
5, 6
5, 7
5, 8
5, 9
5, 10
6, 1
6, 2
6, 3
6, 4
6, 5
6, 7
6, 8
6, 9
6, 10
7, 1
7, 2
7, 3
7, 4
7, 5
7, 6
7, 8
7, 9
7, 10
8, 1
8, 2
8, 3
8, 4
8, 5
8, 6
8, 7
8, 9
8, 10
9, 1
9, 2
9, 3
9, 4
9, 5
9, 6
9, 7
9, 8
9, 10
10, 1
10, 2
10, 3
10, 4
10, 5
10, 6
10, 7
10, 8
10, 9
© 2016 Bridgepoint Education, Inc. All rights reserved. Not for resale or redistribution.
tan82773_04_ch04_091-120.indd 94
3/3/16 2:30 PM
Section 4.1
Distribution of Sample Means
For each possible pair of scores, if we calculate a mean and plot the value in a frequency distribution as a test of the central limit theorem, the result is Figure 4.2. Because the entire
distribution is based on sample means, Figure 4.2 is a distribution of sample means. Strictly
speaking, this distribution is not normal, but although based on precisely the same data, Figure 4.2’s distribution is a good deal more normal than the distribution in Figure 4.1.
Figure 4.2: A frequency distribution of the means of all possible pairs of scores
1 through 10
A distribution of the means of each possible pair of scores with values between 1 and 10. This
distribution is not normal, but has more normality than the distribution shown in Figure 4.1.
10
Score Frequency
9
8
7
6
5
4
3
2
1
1.5
2.0
2.5
3.0
3.5
4.0
4.5
5.0
5.5
6.0
6.5
7.0
7.5
8.0
8.5
9.0
9.5
Sample Means
Mean of the Distribution of Sample Means
The symbol used for a population mean to this point, µ, is actually the symbol for a population
mean formed from one score at a time. To distinguish between the mean of the population of
individual scores and the mean of the population of sample means, we’ll subscript µ with an
M: µM. This symbol indicates a population mean (µ) based on sample means (M).
With a distribution of just 90 sample means, Figure 4.2 shows nothing like an infinite number, of course, but it is instructive nevertheless. The mean of the scores 1 through 10 is 5.5
(µ 5 5.5). Study Figure 4.2 for a moment. What is the mean of that distribution? The mean of
our distribution of sample means is also 5.5: µM 5 5.5. The point is this: When the same data
are used to create two distributions—one a population based on individual scores and the
other a distribution of sample means—the two population means will have the same value, or, symbolically
stated: µ 5 µM.
Try It!: #1
Describing the distribution as “normal” is a stretch, but
Figure 4.2 is certainly more normal than Figure 4.1. For
one thing, rather than the perfectly flat distribution that
occurs when all the scores have the same frequency,
Why is there less variability in the distribution of sample means than in a distribution of individual scores?
© 2016 Bridgepoint Education, Inc. All rights reserved. Not for resale or redistribution.
tan82773_04_ch04_091-120.indd 95
3/3/16 2:30 PM
Distribution of Sample Means
Section 4.1
some scores have greater frequency than others. The sample means near the middle of the
distribution in Figure 4.2 occur more frequently than the sample means at either the extreme
right or left.
Why are extreme scores less likely than scores near the middle of the distribution? It is because
many combinations of scores can produce the mean values in the middle of the distribution,
but comparatively few combinations can produce the values in the tails of the distribution.
With repetitive sampling, the mean scores that can be produced by multiple combinations
increase in frequency and the more extreme scores occur only occasionally, which the next
section illustrates.
Variability in the Distribution of Sample Means
In the original distribution of 10 scores (Figure 4.1), what is the probability that someone
could randomly select one score (x) that happens to have a value of 1? Because there are 10
scores, and just one score of 1, the probability is p 5 1/10 5 0.1, right? By the same token,
what is the probability of selecting x 5 10? It is the same, p 5 0.1.
Moving to the distribution based on 90 scores (Figure 4.2), what is the probability of selecting a sample of n 5 2 that will have M 5 1.0? Is there any probability of selecting two scores
out of the 10 that will have M 5 1.0? Because there is only one value of 1, there is no way
to select two values with M 5 1.0. As soon as a score of 1 is averaged with any other score
in the group, all of which are greater than one, the result is M . 1. That is why the lowest
possible mean score in Figure 4.2 is 1.5, which can only occur when 1 and 2 are in the same
sample.
The same thing occurs in the upper end of the distribution. The probability of selecting a
group of n 5 2 with M 5 10 is also zero (p 5 0) because all other scores have lower values
than 10. For the 90 possible combinations, the highest possible mean score is 9.5, which can
occur only when the 10 and the 9 happen to be in the same sample.
The point is that variability in group scores is always less than the variability in individual
scores. A related point is that the impact of the most extreme scores in a distribution diminishes when they are included in samples with less extreme scores. Applied, these principles
mean that a researcher examining, for example, problem-solving ability among a group
of subjects can afford to be less concerned about the impact of one extremely low or one
extremely high score as the size of the group increases. Larger group sizes minimize the effect
of extreme scores.
Standard Error of the Mean
Recall that the sigma, σ, indicates a population’s standard deviation. Specifically, σ indicates a
standard deviation from a population of individual scores. The symbol for the standard deviation in a distribution of sample means is σM and as the subscript M suggests, it measures variability among the sample means. The formal name for σM is the standard error of the mean.
In the language of statistics, error as in standard error of the mean refers to unexplained variability. As we move through the different procedures, we will calculate other standard errors,
which all have this in common: all are measures of unexplained data variability.
© 2016 Bridgepoint Education, Inc. All rights reserved. Not for resale or redistribution.
tan82773_04_ch04_091-120.indd 96
3/3/16 2:30 PM
Distribution of Sample Means
Section 4.1
Earlier, we noted that whether charting the distribution of individual scores or the distribution of sample means, the means of the two distributions will always be equal: µ 5 µM. Is it
logical to expect the same from the measures of variability; in other words, will σ 5 σM? The
fact that the distribution of individual scores always has more variability than the distribution of sample means answers this question. Symbolically speaking, σ . σM, something that
the dogmatism data show.
The standard deviation of the 10 original scores (1, 2, 3, 4, 5, 6, 7, 8, 9, 10) is σ 5 2.872. Note
that this instance and the calculation of the standard error of the mean just below deal with
populations and the formula must, therefore, employ N, rather than n 2 1. Elsewhere in the
book, however, the formula will always be n 2 1.
The standard error of the mean can be calculated by taking the standard deviation of the
mean scores of each of those 90 samples which constituted the distribution of sample means.
The calculation is a little laborious, and happily, not a pattern that must be followed later, but
the value is σM 5 1.915.
So, as predicted, σ has a larger value than σM. The smaller value for σM reflects the way less
extreme scores moderate the more extreme scores when they occur in the same sample.
Sampling Error
Although the standard error of the mean does not per se refer to a mistake, another kind
of error, sampling error, does. In inferential statistics, samples are important for what they
reveal about populations. However, information from the sample is helpful for drawing inferences only when the sample accurately represents the population. The degree to which the
sample does not represent the population is the degree of sampling error.
Samples reflect the population with the greatest fidelity when two prerequisites are met:
1) the sample must be relatively large, and 2) the sample must be based on random selection.
The safety of large samples is explained by the law of large numbers. According to this
mathematical principle, as a proportion of the whole, errors diminish as the number of data
points increases. The potential for serious sampling error diminishes as the size of the sample
grows. The text earlier referred to this principle in noting that the distorting effect of extreme
scores diminishes as sample size grows.
Random selection refers to a situation where every member of the population has an equal
probability of being selected. Random selection contrasts with what are called convenience
samples, samples that are used intact because they are handy. A sociology professor who uses
the students in a particular section of his class is relying on a type of convenience sample
known as a nonrandom sample.
A random sample of n 5 5 could be created from the 10 people being treated for dogmatic
behavior by assigning each person a number, placing the 10 numbers into a paper bag, shaking the bag well, and without looking, drawing out five numbers.
The result would be a randomly selected sample. When randomly selected, samples differ
from populations only by chance. They will differ, of course, but the differences are less and
less important as sample size grows.
© 2016 Bridgepoint Education, Inc. All rights re…
Essay Writing Service Features
Our Experience
No matter how complex your assignment is, we can find the right professional for your specific task. Achiever Papers is an essay writing company that hires only the smartest minds to help you with your projects. Our expertise allows us to provide students with high-quality academic writing, editing & proofreading services.
Free Features
Free revision policy
$10Free bibliography & reference
$8Free title page
$8Free formatting
$8How Our Dissertation Writing Service Works
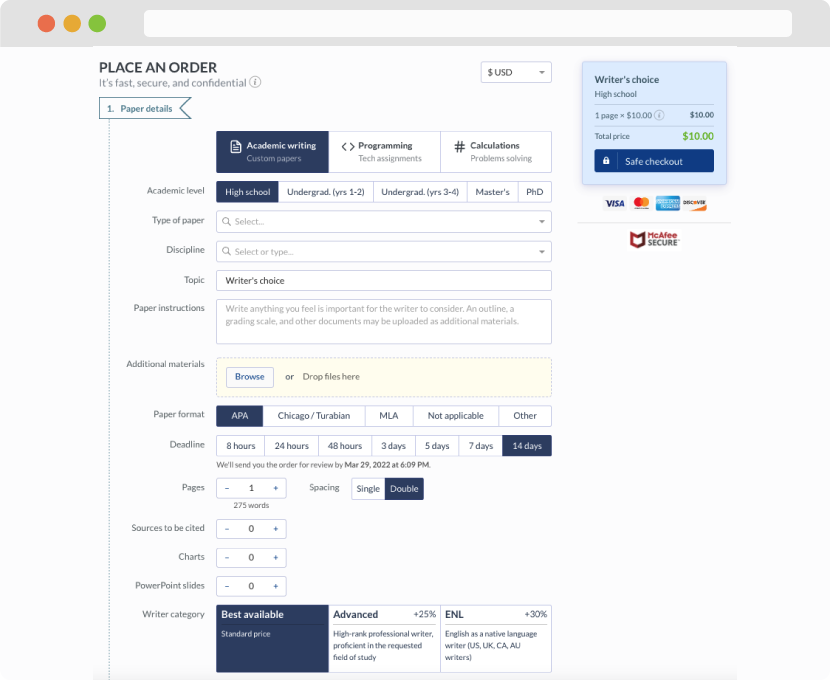
First, you will need to complete an order form. It's not difficult but, if anything is unclear, you may always chat with us so that we can guide you through it. On the order form, you will need to include some basic information concerning your order: subject, topic, number of pages, etc. We also encourage our clients to upload any relevant information or sources that will help.
Complete the order form
Once we have all the information and instructions that we need, we select the most suitable writer for your assignment. While everything seems to be clear, the writer, who has complete knowledge of the subject, may need clarification from you. It is at that point that you would receive a call or email from us.
Writer’s assignment
As soon as the writer has finished, it will be delivered both to the website and to your email address so that you will not miss it. If your deadline is close at hand, we will place a call to you to make sure that you receive the paper on time.
Completing the order and download