Math 138 –O’Donnell.
Hand-In Homework
Health
See the General Instructions in the Course Policy for instructions.
NOTE: For any assigned exercise in the text, if you see a “T” with an orange circle
next to the problem number, the dataset is in StatCrunch.
You do not have to type the
data in. Enter StatCrunch using the button in CourseCompass, go to the given chapter
and look for the name that most closely matches the subject of the exercise.
If you wish additional practice in a given chapter, feel free to look at the exercises in
the other homework packets. For some chapters, I also have a suggested list of “For
extra practice” exercises from the text. These do not have to be handed in and there
is no extra credit for completing them; they are for your benefit only. However, I
will be happy to answer a question on any exercise.
Chapter 2: Data
02.HE.A: Page 17, # 4
02.HE.B (Note: Refer to the instructions on page 17, left hand column, about
halfway down the page. You are required to do only this exercise for B.) Medical
researchers at a large hospital are investigating the impact of a new type of chemotherapy
on four types of blood cancer. From 2000 to 2005 they collected data on 461 patients.
They tracked the age and sex of the patient, type of cancer, stage (1 through 4), and
whether the patient responded to treatment. If the patient responded but relapsed, the
number of days from last treatment until relapse was also tracked. If the patient did not
respond, the number of days from last treatment to death was tabulated.
Chapter 3: Displaying and Describing Categorical Data
03.HE.A: Page 41, #13. Create both a bar chart and a pie chart. Tell what is apparent
from each but not the other.
03.HE.B: Use the table for Exercise 35 on page 44 to answer the following questions.
Give both a fraction and a percent:
(a) What percent of patients were over 50?
(b) What percent of patients had high blood pressure?
(c) What percent of patients were over 50 and had high blood pressure?
(d) What percent of patients with high blood pressure were over 50?
(e) What percent of patients over 50 had high blood pressure?
(f) Do you believe that there is no relationship between age and blood pressure? Use
statistics to justify your answer.
Chapter 4: Displaying and Summarizing Quantitative Data
04.HE.A1: Dr. Paul Oswiecnski randomly selects 20 of his 20 to 29 year old patients and
obtains the following data regarding their serum HDL cholesterol:
70 56 48 48 53 52 66 48 36 49
28 35 58 62 45 60 38 73 45 51
I hope to post these data for StatCrunch on CE6 – check there before typing it in.
a) Make an appropriate display of these data.
b) Find the mean and median.
c) Find the range, variance and standard deviation.
d) Describe any unusual features of the data.
NOTE: Save these data. They will be used again in Exercises 05.HE.A and 06.HE.A.
04.HE.B2 Fourteen different second-year medical students at Belleview Hospital in New
York City measured the blood pressure of the same person. The systolic readings in
mmHg are:
138 130 135 140 120 125 120 130 130 144 143 140 130 150
I hope to post these data for StatCrunch on CE6 – check there before typing it in.
Follow the instructions of 04.HE.A for these data.
a) Draw a histogram of the data.
b) Describe any unusual features of the data.
c) Find the five-number summary.
d) Draw a stem and leaf plot.
e) Which pictorial display do you like better? Why?
Chapter 5: Understanding and Comparing Distributions
05.HE.A: We wish to compare the data set of Exercise 04.HE.A with the serum HDL
cholesterol readings of another twenty of Dr. Oswiecnski’s patients. The second group
follows:
56 51 46 39 56 32 44 60 51 44
63 50 46 69 53 70 33 54 55 52
I hope to post these data for StatCrunch on CE6 – check there before typing it in.
(a) Calculate appropriate summary statistics for the above group..
(b) Draw histograms of these data separately 04.HE.A and 05.HE.A).
(c) Draw side-by-side boxplots.
(d) What is apparent from the boxplots that is not apparent in the histograms?
(e) What is apparent from the histograms that is not apparent in the boxplots.
NOTE: Save these data. They will be used again in Exercise 06.HE.A.
1 Data are from page 151 of “Statisti s: Informed Decisions Using Data” by Michael Sullivan, © 2007,
Pearson.
2 Based on an exercise Sections 2.2 and 2.3 of “Biostatistics” by Triola and Triola
05.HE.B: Page 111, # 12 (You may, if you wish, refer to the data set “Tendon
Transfers” under Chapter 5 of the Course Compass version of StatCrunch. You do not
have to see these data to complete the exercise, however.)
Chapter 6: The Standard Deviation as a Ruler
06.HE.A: For the cholesterol data of Exercise 05.HE.A,
a) Find the mean and standard deviation of these data.
b) Do a normal probability plot (QQ plot).
c) Draw a histogram of the 20 cholesterol readings.
d) Using the actual data, find the number of patients with cholesterol reading higher
than 54. Then divide by 20 to get a percent.
e) Calculate the z-score of the patient with the reading of 54.
f) Using the z-score, find the percent of patients with cholesterol readings higher
than the patient with the reading of 54.
Do the data appear normal? Explain
06.HE.B3 : Birth weights in Norway are normally distributed with a mean weight of 3.75
kg. and a standard deviation of 0.5 kg. A hospital plans to set up a special observation
conditions for the lightest 2% of newborns. What weight is used for the cutoff separating
the lightest 2% from the others?
Practice exercises (whatever you have time for –not to be handed in):
Pages 151-153, 39 through 56.
Chapter 6 exercises in any of the other packets.
3 Triola and Triola, “Biostatistics”, Section 5.3
Chapter 7: Scatterplots, Association and Correlation
07.HE.A: Measurements were made of Hemoglobin4 levels and packed cell volume 5of
21 patients aged 21 to 67 These data are in CE6. 6
a. Make a scatterplot of the data, considering PCV as the independent
variable and Hb as the dependent variable.
b. Calculate the correlation coefficient between PCV and Hb.
c. Write a short report describing the association.
d. Have we proved that a higher packed cell volume causes hemoglobin to
rise?
NOTE: These data will also be used in Exercise 8.HE.A. Also, this is meant to be one
table. I have entered it this way to save space (and paper.)
PCV 25 30 30 33 35 35 39 40
Hb 9.6 10.3 13.1 12.5 12 13.5 10.4 13.9
PCV 40 41 41 44 47 47 46
Hb 16.5 15.8 16.2 15.5 12.4 13 16.4
PCV 46 48 50 50 53 54 54
Hb 16.4 16.1 17.3 17.3 14.2 17.1 17.1
07.HE.B: Page 191, # 36
4 Hemoglobin is the protein molecule in red blood cells that carries oxygen from the
lungs to the body’s tissues and returns carbon dioxide from the tissues to the lungs. The
iron contained in hemoglobin is responsible for the red color of blood. A low
hemoglobin is referred to as being anemic. There are many reasons for anemia. Higher
than normal hemoglobin levels can be seen in people living at high altitudes and in
smokers.
Packed cell volume is the ratio of the volume occupied by packed red blood cells to the
volume of the whole blood as measured by a hematocrit
6 The notes on the cited source only showed the scatterplot, the regression line and 10 of
the 21 data points/ I estimated the other 11 from visually inspecting these, so the data are
probably not precisely accurate.
Chapter 8: Linear Regression
08.HE.A: For the data of Exercise 07.HE.A,
a) Find the equation of the regression line.
b) Interpret the R2.
c) Interpret the slope in context.
d) Find the residual of the patient with a PCV of 44.
e) Overall, is this a good linear fit? Explain.
08.HE.B: Page 222, # 50
Chapters 9 and 10 will not be covered.
Chapter 11: Understanding Randomness
11.HE.A: According to WikiAnswers, 45% of Americans have type O blood; 41% have
type A blood; 11% have type B blood and 3% have type AB blood.
(a) Using integers 0 to 99, devise a scheme for simulating Americans with red blood.
(b) Run 10 simulations on eight patients.
(c) In how many of your simulations was there more than one person with Type B
blood?
11.HE.B : Page 301, # 28
Chapter 12: Sample Surveys
12.HE.A:
(a) Explain in your own words the difference between a parameter and a statistic.
(b) Determine whether the given value is a parameter or a statistic:
(1) There are a total of 453,000 cases of non-Hodgkin’s lymphoma in the
United States.
(2) A sample of thirty cancer patients was surveyed in the waiting room of a
University Cancer Center. Of the 30, eight had non-Hodgkin’s
lymphoma.
12.HE.B7: Students are required to have all of their current vaccinations before starting a
school year. Three days after the start of school, the Central Office for the school system
decides to check on compliance with the rules. They have a list of kindergartners from
each of the 30 schools. What sampling method did the Central Office use?
a. Put the lists together; alphabetize the entire list and take 50 kindergartners at
random.
b. Put the lists together, pick a random number between 1 and 20, take the
kindergartner that far down the list and every 100th thereafter.
c. Go to every school Nurse’s office and check the records of 50 kindergartners
selected at random.
d. At a picnic for all school kindergartners and their families, ask the names of first
200 kindergartners who arrive; and then check their records.
e. Check the record of every kindergartner.
f. Go to one school and check the record of every kindergartner at the school.
Chapter 13: Experiments and Observational Studies
13.HE.A: Page 351, # 12 (Note: Refer to the instructions on page 350, right column,
about 2/3 of the way down the page for this exercise.)
13.HE.B: Page 354, # 46. In addition, design a retrospective observational study and a
prospective observational study.
Chapter 14: From Randomness to Probability
14.HE.A: Page 382, #32
14.HE.B: Page 382, #34
Additional practice exercises (whatever you have time for –not to be
handed in): Pages 379 – 383, # 1, 3, 7, 11, 15, 19 and 21, 35, and 41
Chapter 15: Probability Rules!
15.HE.A:Page405, #25
7 Exercises in Section 1.2 of Triola, “Elementary Statistics’
15.HE.B8: In a study of the relationship between health risk and income9, a large group
of Massachusetts residents were asked a series of questions. The responses to two of
these questions are tabulated below. Here, “stressed” means that the respondent reported
that most days are “extremely stressful” or “quite stressful”, while “not stressed” means
that the respondent reported, “a bit stressful”, “not very stressful” or “not at all stressful.”
Stress
Level
Income
Low Medium High Total
Stressed 526 274 216 1016
Not stressed 1954 1680 1899 5533
Total 2480 1954 2115 6549
a) What is the probability that someone in the study has low income?
b) What is the probability that someone in the study is stressed?
c) What is the probability that someone in the study is stressed and has low income?
d) What is the probability that someone in the study is stressed given that the
respondent has low income?
e) What is the probability that someone in the study has low income given that the
respondent is stressed?
f) Are stress level and income independent? Explain.
Additional practice exercises (whatever you have time for –not to be
handed in): Pages 4404 – 408, # 1 and 21, 5 and 11, 9 and 27, 15, 17, 19,
31, 43.
Don’t forget Exercise 15.HE.C on the next page!
8 Exercise 3.13, Samuels & Witner, “Statistics for the Life Sciences”, 3rd edition, Prentice-Hall, 2003
9 Adapted by the authors (above footnote) from Taira, DA, Gafran, DG, Seto, TB, Rogers, WH and Tarlow,
AB, “The Relationship Between Patient Income and Physician Discussion of Health Risk Behaviors”,
Journal of the American Medical Association, 278 (1997), 1412-1417
15.HE.C: According to Jessica M. Utts PhD (“Seeing Through Statistics”, © 19999,
Duxbury Press, page 303), “To determine the probability of a positive test result being
accurate, you need only three pieces of information:
1. The base rate or probability that you are likely to have the disease without any
knowledge of your test results.
2. The sensitivity of the test, which is the proportion of people who correctly test
positive when they actually have the disease.
3. The specificity of the test, which is the proportion of people who correctly test
negative when they don’t have the disease.
Data below are from the National Cancer Institute http://www.cancer.gov and links from
that site.
Ladies – complete this part:
The probability of a woman (under 40) being diagnosed with breast cancer is quoted as 1
in 233. (This varies with age, race, family history, etc.) The likely first step in the
diagnosis of suspected breast cancer is a mammogram. A mammogram has 82.4%
sensitivity and 93.2% specificity. What is the probability of a woman having breast
cancer if her mammogram comes back positive? What if it comes back negative?
Gentlemen – complete this part:
The probability of a man having prostate cancer is quoted as 159.9 in 1000. (This varies
with age, race, family history, etc.) The first step in the diagnosis of suspected prostate
cancer is a PSA (protein-specific antigen) laboratory test. Done in conjunction with a
rectal exam by the physician, the PSA has a sensitivity of 34.9% and a specificity of
63.1%. What is the probability of a man in this situation having prostate cancer if his
biopsy comes back abnormally high (this cutoff increases with the patient’s age)? What
if it comes back normal?
Chapter 16: Random Variables
16.HE.A: A hospital emergency room keeps track of the number of patients that need to
be admitted overnight for observation. The staff estimates that the probability model for
the number of ER patients admitted overnight is:
X 0 1 2 3 4 5
P(x) 0.05 0.25 0.35 0.15 0.15 0.05
(a) How many patients does the ER staff expect to be admitted on a given day?
(b) What is the standard deviation?
(c) Over a five-day period, how many patients does the ER staff expect will be
admitted?
(d) What is the standard deviation for the five-day period?
http://www.cancer.gov/
16.HE.B10 For a group of four men, the probability distribution of the number x who live
through the next year is given by the following table:
X 0 1 2 3 4
P(x) 0.0000 0.0001 0.0006 0.0387 0.9606
Find the expected value and standard deviation. Explain these findings in context.
Additional practice exercises (whatever you have time for –not to be
handed in): Pages 427 – 431; # 1 and 11, 2 and 12, 6, 17 and 33, 21, 27, 29,
37, 39 and 41, 47 (Actually, all of the exercises in this chapter are excellent.)
Chapter 17: Probability Models
17.HE.A: A State Dental Society wants to see how many State residents visit their dentist
twice a year as recommended. Based on historical data, it is expected that 60% the
citizens visit their dentist twice a year. Assume that the Dental Society randomly surveys
10 citizens,
(a) What is the probability of the following results:
(1) Exactly six see their dentist twice a year?
(2) At least six see their dentist twice a year?
(3) At most six six see their dentist twice a year?
(b) Find the mean and standard deviation of the number of people who see their
dentist twice a year?
17.HE.B: Now suppose the Dental Society follows up with 1,000 citizens.
(a) Find the mean and standard deviation of the number of citizens who visit their
dentist twice a year.
(b) Is a Normal model appropriate here? Explain.
(c) Use the 68-95-99.7 rule to describe this distribution.
(d) Would the Dental Society be surprised if there were only 500 citizens who visit
their dentist twice a year? Explain using your answer to (c)
Additional practice exercises (whatever you have time for –not to be
handed in): Pages 447 – 451, # 1, 3, 17, 20 d through f, 22 a and b, 24, 27,
31, 38, 43
Chapter 18: Sampling Distribution Models
18.HE.A:Page 481, #24.
10 Based on an exercise Section 4.2 of “Biostatistics” by Triola and Triola
18.HE.B11 For men between 18 and 24 years, serum cholesterol12 levels (in mg/100mL)
have a mean of 178.1 and a standard deviation of 40.7 (based on data from the National
Health Survey.)
(a) Find the percentage of males aged 23, who have a serum cholesterol level of
210mg/100mL (or above). Is this level unusually high?
(b) In a group of 25 males aged 23, what is the probability that the mean serum
cholesterol level is210mg/100mL (or above). Is this level unusually high?
Discuss the assumptions and conditions that support your model, and draw a suitably
labeled diagram.
Please read — General Instructions for Chapters 19 through 26:
• For confidence intervals, use 95% unless otherwise specified.
• For hypothesis testing, use the α-level 0.05 unless otherwise specified.
• Give p-values to four decimal places. Reminder: if the technology reports p = 0,
you should report p < 0.0001 since a p-value cannot be 0. Chapter 19: Confidence Intervals for Proportions 19.HE.A: Page 507, #40 19.HE.B: Page 506, # 26 19.HE.C: I normally present an example of a direct application of the methods of this
chapter to current events.
(a) Find another one. Cite the source, explain clearly what question the source is
answering, give the number (n) and give the percent “success” (p). The source
will most likely not give an exact number of “success responses”, so assume one
by multiplying n by p and rounding.
(b) Find a 95% confidence interval for the answer to the question. State the
conclusion in context.
(c) Compute the margin of error. If the source states a margin of error, say whether
this number is correct.
Here is some guidance on where to look.
Gallup: http://www.gallup.com
Rasmussen: http://www.rasmussenreports.com/
Pew Research: http://pewresearch.org/
Gonzales Research (Annapolis) http://www.gonzalesresearch.com/poll_directory.html
Quinnipac University (Connecticut): http://www.quinnipiac.edu/x271.xml
11 Based on an exercise Sections 2.2 and 2.3 of “Biostatistics” by Triola and Triola
12 Cholesterol is different from most tests in that it is not used to diagnose or monitor a
disease but is used to estimate risk of developing a disease — specifically heart disease.
Because high blood cholesterol has been associated with hardening of the arteries, heart
disease and a raised risk of death from heart attacks, cholesterol testing is considered a
routine part of preventive health care.
https://owa.howardcc.edu/owa/redir.aspx?C=c2cfc3cd2f394d2ea1c892eba14fc9f9&URL=http%3a%2f%2fwww.gallup.com%2f
https://owa.howardcc.edu/owa/redir.aspx?C=c2cfc3cd2f394d2ea1c892eba14fc9f9&URL=http%3a%2f%2fwww.rasmussenreports.com%2f
https://owa.howardcc.edu/owa/redir.aspx?C=c2cfc3cd2f394d2ea1c892eba14fc9f9&URL=http%3a%2f%2fpewresearch.org%2f
https://owa.howardcc.edu/owa/redir.aspx?C=c2cfc3cd2f394d2ea1c892eba14fc9f9&URL=http%3a%2f%2fwww.gonzalesresearch.com%2fpoll_directory.html
https://owa.howardcc.edu/owa/redir.aspx?C=c2cfc3cd2f394d2ea1c892eba14fc9f9&URL=http%3a%2f%2fwww.quinnipiac.edu%2fx271.xml
You could also Google (or Bing)
NBC News Poll 2011 (or 2012)
ABC News Poll 2011 (or 2012)
CBS News Poll 2011 (or 2012)
FOX News Poll 2011 (or 2012)
New York Times Poll 2011 (or 2012)
(almost any large newspaper) Poll 2011 (or 2012)
Putting in 2011 (or 2012) will get you the more recent polls.
Chapter 20: Hypothesis Testing
20.HE.A:13 It is estimated that 1% of the population suffers from red/green color
blindness (Source: USA Today). The ophthalmology department of a large
university medical center randomly tests 300 men. 11 are found to have this type
of color blindness.
(a) Check the necessary assumptions and conditions for a confidence interval.
(b) Compute a 95% confidence interval estimate of the proportion of all me with this
type of color blindness.
(c) State your conclusion in context.
(d) What sample size would be needed to estimate the proportion of male red / green
color blindness if we wanted 96% confidence that the margin of error is no more
than 3%, assuming the data from the exercise?
(e) If we make the (very unrealistic) assumption that half of the 300 were colorblind,
what sample size should we then need for subsequent studies if we want no more
than a 3% margin of error.
20.HE.B: For the color blindness data above, we wish to test a hypothesis to answer the
question, “Has the instance of color blindness increased from the historical rate of 1%?”
(a) Write appropriate hypotheses.
(b) Check the necessary assumptions and conditions for the test, given that we
completed Exercise A? Why or why not?
(c) Perform the test. What is the p-value?
(d) Explain carefully what the p-value means in this context.
(e) What is your conclusion? (Use alpha-level 0.05.)
Suggestions for additional practice (text exercises): Exercises 1 through 10 at the end
of Chapter 20 are good for basic concepts. Exercises 11 and 12 may confuse more than
enlighten! Exercises 13 through the end are all good. For any of the later exercises that
ask for a hypothesis test, it would be good practice to also compute a confidence interval
at the same level as the test (i.e. hypothesis test at the 5% level -> 95% confidence
interval.)
13 Triola, “Elementary Statistics”, Sec. 8-4
Chapter 21: Type I and II errors
21.HE.A:For the situation described in Exercise 18 on page 553, instead of answering
their questions, answer the following:
(a) Is this a one-tailed or a two-tailed test? Explain. Write the appropriate
hypotheses (Ho and Ha.)
(b) Write the null and alternative hypotheses. Remember that the null hypothesis is
an indication of no effect.
(c) In this context, what would a Type I error be? What are the consequences?
(d) In this context, what would a Type II error be? What are the consequences?
All of the text exercises in Chapter 21 are good for additional practice. Keep in mind that
you can safely skip question parts that involve power, as you will not be responsible for
this concept on the assessments.
Chapter 22: Comparing Two Proportions
22.HE.A:Page 576, #20. Instead of (f), compute a 95% confidence interval and explain
the interval in context.
22.HE.B: 14When treating carpal tunnel syndrome, should a patient be treated with
surgery or should a splint be applied? In a study of this issue, 73 patients were treated
with surgery and 83 were treated with a splint. After 12 months, success was noted in 67
of the surgery patients and 60 of the splint patients15. Go through “The Drill” for the
data in this exercise.
22.HE.C I will motivate this chapter by presenting another example of a direct
application of the methods of this chapter to current events. In this chapter, you will
need to locate two surveys a time period apart (say a week, a month, a year, etc.) in
which the same question is asked. You will explore the difference in the response using
the methods of Chapter 22. One of the surveys can be the same one you used for
Chapter 19.
(a) Locate the surveys. Cite the source, explain clearly what question the source is
answering, give the number (n) and give the percent “success” (p) in both
surveys. The source will most likely not give an exact number of “success
responses”, so assume one by multiplying n by p and rounding.
(b) Find a 95% confidence interval for the answer to the question. State the
conclusion in context.
(c) Compute the margin of error for the difference in response. If the source states a
margin of error, say whether this number is correct.
(d) Test at alpha-level 0.05 the hypothesis that there is no difference in the response
rate between the first and second survey. State your conclusion in context.
14 Triola, “Elementary Statistics”, Intro to Chapter 9
15 Based on data from “Splinting vs. Surgery in the Treatment of Carpal Tunnel Syndrome” by Gerritsen et.
al., Journal of the American Medical Association, Vol. 288, No. 10.
Here is some guidance on where to look.
Gallup: http://www.gallup.com
Rasmussen: http://www.rasmussenreports.com/
Pew Research: http://pewresearch.org/
Gonzales Research (Annapolis) http://www.gonzalesresearch.com/poll_directory.html
Quinnipac University (Connecticut): http://www.quinnipiac.edu/x271.xml
You could also Google (or Bing)
NBC News Poll 2011 (or 2012)
ABC News Poll 2011 (or 2012)
CBS News Poll 2011 (or 2012)
FOX News Poll 2011 (or 2012)
New York Times Poll 2011 (or 2012)
(almost any large newspaper) Poll 2011 (or 2012)
Putting in 2011 (or 2012) will get you the more recent polls.
Chapter 23: One sample t-test
23.HE.A:16 A pre-med student in a statistics class is required to do a class project. She
plans to collect sample data to see if the mean body temperature is 37.0°C (98.6°F) as is
commonly believed. As the authors of the source text humorously say, “Because of time
constraints imposed by other courses and the desire to maintain a social life that goes
beyond talking in her sleep, she finds that she has time to collect data from only 12
people.” Her data are given below.
36.7 36.4 37.0 37.1 36.7 36.9 37.0 37.5 36.9 37.1 37.0 36.4
(a) Find and interpret in context a 95% confidence interval for the body temperature
data that she has collected.
(b) An article that she recently read makes the claim that mean body temperature is
actually less than 37.0°C (98.6°F). Test that claim and explain your conclusion in
context.
(c) Comment on each of the assumptions and conditions (make a picture for the
nearly normal condition).
23.HE.B: Suppose a pilot study is conducted using data from 15 heavy ice-cream eating
students who just bought four-scoop banana splits! The study measures blood
cholesterol levels on the 15 ice cream eaters: = 205 mg / 100 ml and s = 43 mg /
100 ml. You may assume that assumptions and conditions were met.
1. Construct and interpret a 95% confidence interval for .
2. Test the hypothesis that the population mean cholesterol level is 170 or less.
3. State your conclusions to 1 and 2 in context.
16 Based on an example on page 355 of Triola& Triola “Biostatistics”, Pearson © 2006.
https://owa.howardcc.edu/owa/redir.aspx?C=c2cfc3cd2f394d2ea1c892eba14fc9f9&URL=http%3a%2f%2fwww.gallup.com%2f
https://owa.howardcc.edu/owa/redir.aspx?C=c2cfc3cd2f394d2ea1c892eba14fc9f9&URL=http%3a%2f%2fwww.rasmussenreports.com%2f
https://owa.howardcc.edu/owa/redir.aspx?C=c2cfc3cd2f394d2ea1c892eba14fc9f9&URL=http%3a%2f%2fpewresearch.org%2f
https://owa.howardcc.edu/owa/redir.aspx?C=c2cfc3cd2f394d2ea1c892eba14fc9f9&URL=http%3a%2f%2fwww.gonzalesresearch.com%2fpoll_directory.html
https://owa.howardcc.edu/owa/redir.aspx?C=c2cfc3cd2f394d2ea1c892eba14fc9f9&URL=http%3a%2f%2fwww.quinnipiac.edu%2fx271.xml
23.HE.C17 When testing a claim about a population mean with a sample random sample
selected from a normally distributed population with unknown σ, the Student t-
distribution should be used for finding the critical values and / or p-values. If the
standard normal distribution is incorrectly used with the estimate s of σ, does that mistake
make you more or less likely to reject the null hypothesis, or does it not make a
difference? Explain.
Chapter 24: Two-sample t-test
24.HE.A18 In an experiment designed to test the effectiveness of paroxetine for treating
bipolar depression, subjects are measured using the Hamilton Depression Scale with the
results below19. 43 patients were used in the placebo group; the sample mean was 21.57
and the sample standard deviation was 3.87. The treated group had 33 patients, a sample
mean of 20.38 and s = 3.91. A lower score is better. Go through “The Drill” for
independent t-tests (Use a 95% confidence level and a 0.05 α-level.)
24.HE.B: 20People spend about $5 billion annually in the USA for the purchase of
magnets used to treat a wide variety of pain. Researchers conducted a study to determine
whether magnets are effective in treating back pain. Pain was measured using the visual
analog scale, and the results of the study are obtained below21. The magnet was used
for 20 patients, resulting in a sample mean of 0.49 and a sample standard deviation of
0.96. Also, 20 patients treated with a non-magnetized look-alike instrument, giving a
sample mean of 0.44 and a sample standard deviation of 1.44. Go through “The Drill” for
independent t-tests (Use a 95% confidence level and a 0.05 α-level.)
Chapter 25: Paired t-test
25.HE.A: Page 671, #30
25.HE.B: 22Captopril is a drug designed to lower systolic blood pressure. When
subjects were treated with this drug, their systolic blood pressure readings (in mm Hg)
were measured before and after the drug was taken. The results are in the accompanying
table23.
17 Triola, Elementary Statistics, Exercise 8.5.33
18 Triola, “Elementary Statistics”, Section 9-5
19 Source: “Double-Blind Placebo-Controlled Comparison of Imipramine and Paroxetine
in the Treatment of Bipolar Depression” by Nemeroff, Evans et al, American Journal of
Psychiatry, Vol. 158,No. 6
20 Triola, op cit
21 Source: “Bipolar Permanent Magnets for the Treatment of Chronic Lower Back Pain”
by Collacot et al, Journal of the American Medical Association, Vol. 283, No. 10
22 From Triola, “Elementary Statistics”, Sec. 9-4
23 Source: Essential Hypertension: Effect of a Oral Inhibitor of Angiotension-Converting
Enzyme” by MacGregor et al., British Medical Journal, Vol. 2.
(a) Go through “The Drill” for paired t-tests (Use a 95% confidence level and a 0.05
α-level.)
(b) What p-value do we get if we choose the wrong test? Will it affect the
conclusion?
A B C D E F G H I J K L
Before 200 174 198 170 179 182 193 209 185 155 169 210
After 191 170 177 167 159 151 176 183 159 145 146 177
Chapter 26: Comparing Groups (Chi-square)
26.HE.A24: The individuals in the following table25 have one and only one of the three
types of infection listed:
Age (years)
Infection 18 to 29 30 to 44 45 to 64 65 and Older
Ear 440 567 349 59
Nose 924 1311 794 102
Throat 253 311 157 19
(a) What is the natural question to answer?
(b) Write the null and alternative hypotheses.
(c) How many degrees of freedom should we use in the χ2 test?
(d) Compute the χ2 statistic and p-value.
(e) State the conclusion in context.
26.HE.B26: In a study of peptic ulcer, blood types were determined for 1,665 ulcer
patients in a large hospital ambulatory care canter. The accompanying table shows the
data for this group of patients as well as 10,000 patients who are known not to have this
condition:
(a) What is the natural question to
answer?
(b) Write the null and alternative
hypotheses.
(c) How many degrees of freedom
should we use in the χ2 test?
(d) Compute the χ2 statistic and p-value.
(e) State the conclusion in context.
24 Adapted from Exercise 11.22 of Johnson & Kuby, “Stat”, Brooks-Cole, 2009
25 Centers for Disease Control and Prevention, National Center for Health Statistics,
reported by Johnson & Kuby, Ibid
26 Exercise 10.49amuels & Witmer, “Statistics for the Life Sciences”, Prentice-Hall, 2003
Ulcer Non-Ulcer
O 911 4578
A 579 4219
B 124 890
AB 41 313
26.HE.C:27 Randomly selected birth records are obtained and results are listed in the
table below28.
Sunday Monday Tuesday Wednesday Thursday Friday Saturday
36 55 62 60 60 58 48
(a) Test the claim that births occur with equal frequency on the different days of the
week.
(b) State your conclusion in context.
27 Exercise 11.2.12, Triola, “Elementary Statistics”
28 National Vital Statistics Report, Vol.49, No. 1
Essay Writing Service Features
Our Experience
No matter how complex your assignment is, we can find the right professional for your specific task. Achiever Papers is an essay writing company that hires only the smartest minds to help you with your projects. Our expertise allows us to provide students with high-quality academic writing, editing & proofreading services.
Free Features
Free revision policy
$10Free bibliography & reference
$8Free title page
$8Free formatting
$8How Our Dissertation Writing Service Works
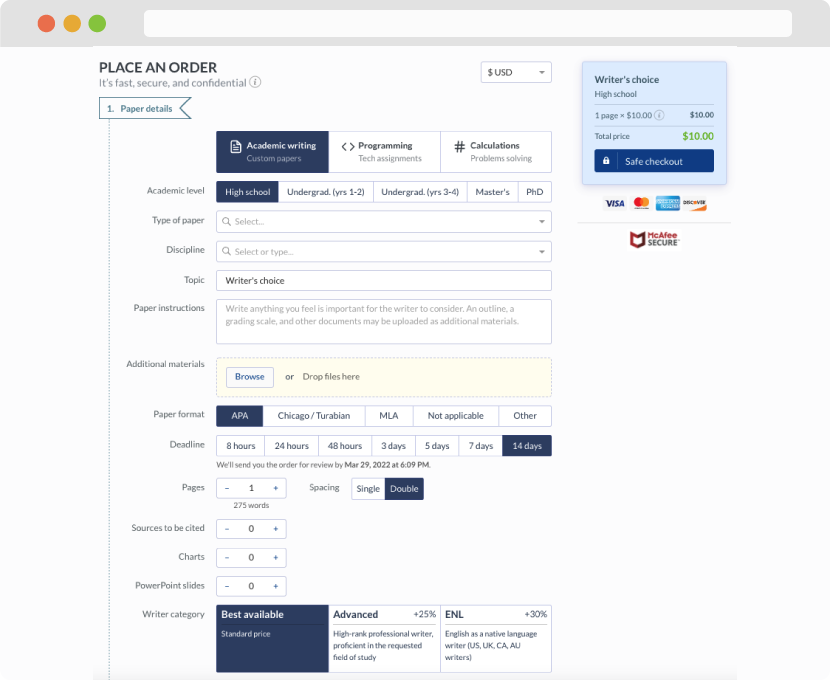
First, you will need to complete an order form. It's not difficult but, if anything is unclear, you may always chat with us so that we can guide you through it. On the order form, you will need to include some basic information concerning your order: subject, topic, number of pages, etc. We also encourage our clients to upload any relevant information or sources that will help.
Complete the order form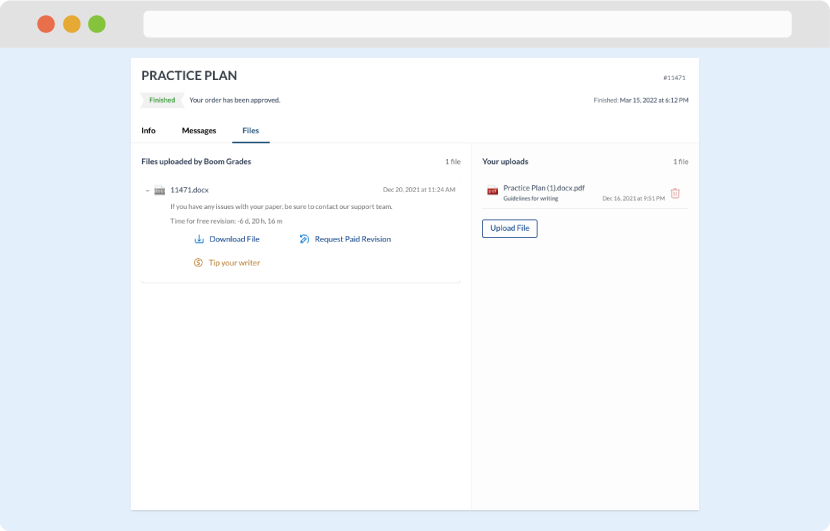
Once we have all the information and instructions that we need, we select the most suitable writer for your assignment. While everything seems to be clear, the writer, who has complete knowledge of the subject, may need clarification from you. It is at that point that you would receive a call or email from us.
Writer’s assignment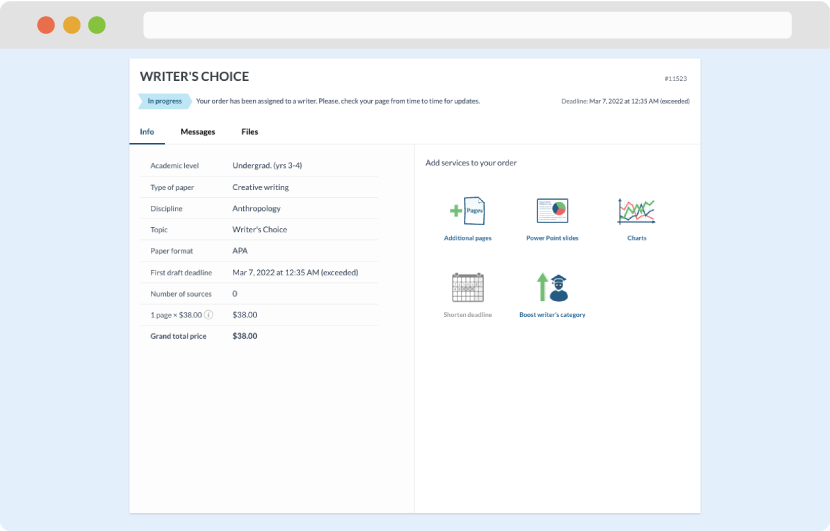
As soon as the writer has finished, it will be delivered both to the website and to your email address so that you will not miss it. If your deadline is close at hand, we will place a call to you to make sure that you receive the paper on time.
Completing the order and download