Can you explain how the GCD (Greatest Common Divisor) works based on lesson #2?
Analysis of algorithms
Issues:
correctness
time efficiency
space efficiency
optimality
Approaches:
theoretical analysis
empirical analysis
Design and Analysis of Algorithms – Chapter 2
Theoretical analysis of time efficiency
Time efficiency is analyzed by determining the number of repetitions of the basic operation as a function of input size
Basic operation: the operation that contributes most towards the running time of the algorithm
T(n) ≈ copC(n)
running time
execution time
for basic operation
Number of times basic operation is executed
input size
Design and Analysis of Algorithms – Chapter 2
Input size and basic operation examples
Problem Input size measure Basic operation
Searching for key in a list of n items Number of list’s items, i.e. n Key comparison
Multiplication of two matrices Matrix dimensions or total number of elements Multiplication of two numbers
Checking primality of a given integer n n’size = number of digits (in binary representation) Division
Typical graph problem #vertices and/or edges Visiting a vertex or traversing an edge
Design and Analysis of Algorithms – Chapter 2
Empirical analysis of time efficiency
Select a specific (typical) sample of inputs
Use physical unit of time (e.g., milliseconds)
or
Count actual number of basic operation’s executions
Analyze the empirical data
Design and Analysis of Algorithms – Chapter 2
Best-case, average-case, worst-case
For some algorithms efficiency depends on form of input:
Worst case: Cworst(n) – maximum over inputs of size n
Best case: Cbest(n) – minimum over inputs of size n
Average case: Cavg(n) – “average” over inputs of size n
Number of times the basic operation will be executed on typical input
NOT the average of worst and best case
Expected number of basic operations considered as a random variable under some assumption about the probability distribution of all possible inputs
Design and Analysis of Algorithms – Chapter 2
Example: Sequential search
Worst case
Best case
Average case
Design and Analysis of Algorithms – Chapter 2
Types of formulas for basic operation’s count
Exact formula
e.g., C(n) = n(n-1)/2
Formula indicating order of growth with specific multiplicative constant
e.g., C(n) ≈ 0.5 n2
Formula indicating order of growth with unknown multiplicative constant
e.g., C(n) ≈ cn2
Design and Analysis of Algorithms – Chapter 2
Order of growth
Most important: Order of growth within a constant multiple as n→∞
Example:
How much faster will algorithm run on computer that is twice as fast?
How much longer does it take to solve problem of double input size?
Design and Analysis of Algorithms – Chapter 2
Example: cn2
how much faster on twice as fast computer? (2)
how much longer for 2n? (4)
Values of some important functions as n
Design and Analysis of Algorithms – Chapter 2
Asymptotic order of growth
A way of comparing functions that ignores constant factors and small input sizes
O(g(n)): class of functions f(n) that grow no faster than g(n)
Θ(g(n)): class of functions f(n) that grow at same rate as g(n)
Ω(g(n)): class of functions f(n) that grow at least as fast as g(n)
Design and Analysis of Algorithms – Chapter 2
Big-oh
Design and Analysis of Algorithms – Chapter 2
Big-omega
Design and Analysis of Algorithms – Chapter 2
Big-theta
Design and Analysis of Algorithms – Chapter 2
Establishing order of growth using the definition
Definition: f(n) is in O(g(n)) if order of growth of f(n) ≤ order of growth of g(n) (within constant multiple),
i.e., there exist positive constant c and non-negative integer n0 such that
f(n) ≤ c g(n) for every n ≥ n0
Examples:
10n is O(n2)
5n+20 is O(n)
Design and Analysis of Algorithms – Chapter 2
Examples:
10n is O(n2)
since 10n ≤ 10n2 for n ≥ 1 or 10n ≤ n2 for n ≥ 10
c n0
5n+20 is O(10n)
since 5n+20 ≤ 10 n for n ≥ 4
c n0
Some properties of asymptotic order of growth
f(n) O(f(n))
f(n) O(g(n)) iff g(n) (f(n))
If f (n) O(g (n)) and g(n) O(h(n)) , then f(n) O(h(n))
Note similarity with a ≤ b
If f1(n) O(g1(n)) and f2(n) O(g2(n)) , then
f1(n) + f2(n) O(max{g1(n), g2(n)})
Design and Analysis of Algorithms – Chapter 2
Establishing order of growth using limits
lim T(n)/g(n) =
Examples:
10n vs. n2
n(n+1)/2 vs. n2
n→∞
0 order of growth of T(n) < order of growth of g(n)
c > 0 order of growth of T(n) = order of growth of g(n)
∞ order of growth of T(n) > order of growth of g(n)
Design and Analysis of Algorithms – Chapter 2
L’Hôpital’s rule and Stirling’s formula
L’Hôpital’s rule: If limn f(n) = limn g(n) = and
the derivatives f´, g´ exist, then
Stirling’s formula: n! (2n)1/2 (n/e)n
Example: log n vs. n
Example: 2n vs. n!
f(n)
g(n)
f ´(n)
g ´(n)
lim
n
=
lim
n
Design and Analysis of Algorithms – Chapter 2
Orders of growth of some important functions
All logarithmic functions loga n belong to the same class
(log n) no matter what the logarithm’s base a > 1 is
All polynomials of the same degree k belong to the same class: aknk + ak-1nk-1 + … + a0 (nk)
Exponential functions an have different orders of growth for different a’s
order log n < order n (>0) < order an < order n! < order nn Design and Analysis of Algorithms - Chapter 2 Basic asymptotic efficiency classes 1 constant log n logarithmic n linear n log n n-log-n or linearithmic n2 quadratic n3 cubic 2n exponential n! factorial Design and Analysis of Algorithms - Chapter 2 Time efficiency of nonrecursive algorithms General Plan for Analysis Decide on parameter n indicating input size Identify algorithm’s basic operation Determine worst, average, and best cases for input of size n Set up a sum for the number of times the basic operation is executed Simplify the sum using standard formulas and rules (see Appendix A) Design and Analysis of Algorithms - Chapter 2 Useful summation formulas and rules liu1 = 1+1+ ⋯ +1 = u - l + 1 In particular, liu1 = n - 1 + 1 = n (n) 1in i = 1+2+ ⋯ +n = n(n+1)/2 n2/2 (n2) 1in i2 = 12+22+ ⋯ +n2 = n(n+1)(2n+1)/6 n3/3 (n3) 0in ai = 1 + a + ⋯ + an = (an+1 - 1)/(a - 1) for any a 1 In particular, 0in 2i = 20 + 21 + ⋯ + 2n = 2n+1 - 1 (2n ) (ai ± bi ) = ai ± bi cai = cai liuai = limai + m+1iuai Design and Analysis of Algorithms - Chapter 2 Example 1: Maximum element Design and Analysis of Algorithms - Chapter 2 Example 2: Element uniqueness problem Design and Analysis of Algorithms - Chapter 2 Example 3: Matrix multiplication Design and Analysis of Algorithms - Chapter 2 Example 4: Gaussian elimination Algorithm GaussianElimination(A[0..n-1,0..n]) //Implements Gaussian elimination of an n-by-(n+1) matrix A for i 0 to n - 2 do for j i + 1 to n - 1 do for k i to n do A[j,k] A[j,k] - A[i,k] A[j,i] / A[i,i] Find the efficiency class and a constant factor improvement. Design and Analysis of Algorithms - Chapter 2 Example 5: Counting binary digits It cannot be investigated the way the previous examples are. Design and Analysis of Algorithms - Chapter 2 Plan for Analysis of Recursive Algorithms Decide on a parameter indicating an input’s size. Identify the algorithm’s basic operation. Check whether the number of times the basic op. is executed may vary on different inputs of the same size. (If it may, the worst, average, and best cases must be investigated separately.) Set up a recurrence relation with an appropriate initial condition expressing the number of times the basic op. is executed. Solve the recurrence (or, at the very least, establish its solution’s order of growth) by backward substitutions or another method. Design and Analysis of Algorithms - Chapter 2 Example 1: Recursive evaluation of n! Definition: n ! = 1 2 … (n-1) n for n ≥ 1 and 0! = 1 Recursive definition of n!: F(n) = F(n-1) n for n ≥ 1 and F(0) = 1 Size: Basic operation: Recurrence relation: Design and Analysis of Algorithms - Chapter 2 Note the difference between the two recurrences. Students often confuse these! F(n) = F(n-1) n F(0) = 1 for the values of n! ------------ M(n) =M(n-1) + 1 M(0) = 0 for the number of multiplications made by this algorithm Solving the recurrence for M(n) M(n) = M(n-1) + 1, M(0) = 0 Design and Analysis of Algorithms - Chapter 2 Example 2: The Tower of Hanoi Puzzle Recurrence for number of moves: Design and Analysis of Algorithms - Chapter 2 Solving recurrence for number of moves M(n) = 2M(n-1) + 1, M(1) = 1 Design and Analysis of Algorithms - Chapter 2 Tree of calls for the Tower of Hanoi Puzzle Design and Analysis of Algorithms - Chapter 2 Example 3: Counting #bits Design and Analysis of Algorithms - Chapter 2 Fibonacci numbers The Fibonacci numbers: 0, 1, 1, 2, 3, 5, 8, 13, 21, … The Fibonacci recurrence: F(n) = F(n-1) + F(n-2) F(0) = 0 F(1) = 1 General 2nd order linear homogeneous recurrence with constant coefficients: aX(n) + bX(n-1) + cX(n-2) = 0 Design and Analysis of Algorithms - Chapter 2 Solving aX(n) + bX(n-1) + cX(n-2) = 0 Set up the characteristic equation (quadratic) ar2 + br + c = 0 Solve to obtain roots r1 and r2 General solution to the recurrence if r1 and r2 are two distinct real roots: X(n) = αr1n + βr2n if r1 = r2 = r are two equal real roots: X(n) = αrn + βnr n Particular solution can be found by using initial conditions Design and Analysis of Algorithms - Chapter 2 Application to the Fibonacci numbers F(n) = F(n-1) + F(n-2) or F(n) - F(n-1) - F(n-2) = 0 Characteristic equation: Roots of the characteristic equation: General solution to the recurrence: Particular solution for F(0) =0, F(1)=1: Design and Analysis of Algorithms - Chapter 2 Computing Fibonacci numbers Definition-based recursive algorithm Nonrecursive definition-based algorithm Explicit formula algorithm Logarithmic algorithm based on formula: for n≥1, assuming an efficient way of computing matrix powers. F(n-1) F(n) F(n) F(n+1) 0 1 1 1 = n Design and Analysis of Algorithms - Chapter 2 1 2 3 n n -1 n -1 n -2 n -2 n -2 n -2 1 1 ... ... ... 2 1 1 2 1 1 2 1 1 2
Essay Writing Service Features
Our Experience
No matter how complex your assignment is, we can find the right professional for your specific task. Achiever Papers is an essay writing company that hires only the smartest minds to help you with your projects. Our expertise allows us to provide students with high-quality academic writing, editing & proofreading services.
Free Features
Free revision policy
$10Free bibliography & reference
$8Free title page
$8Free formatting
$8How Our Dissertation Writing Service Works
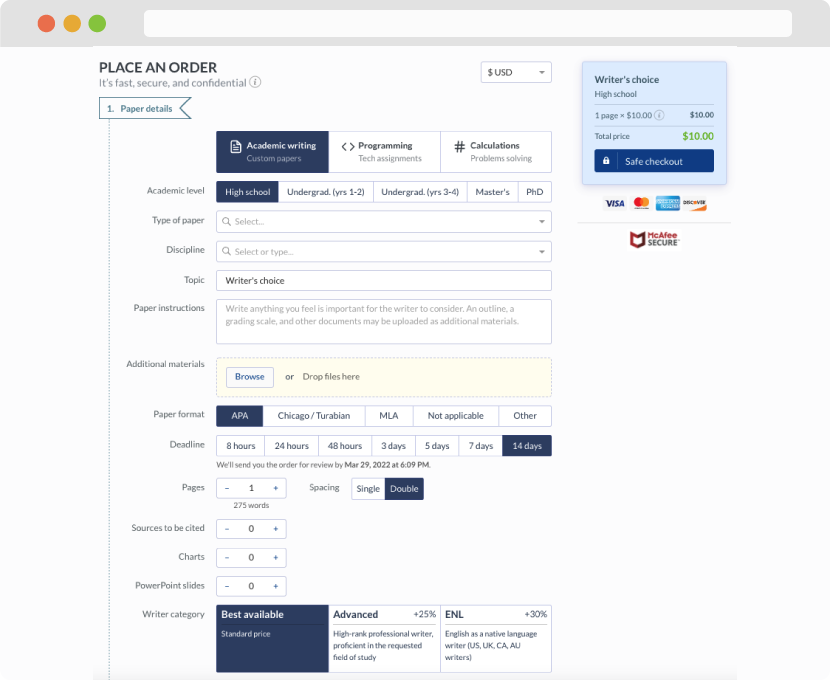
First, you will need to complete an order form. It's not difficult but, if anything is unclear, you may always chat with us so that we can guide you through it. On the order form, you will need to include some basic information concerning your order: subject, topic, number of pages, etc. We also encourage our clients to upload any relevant information or sources that will help.
Complete the order form
Once we have all the information and instructions that we need, we select the most suitable writer for your assignment. While everything seems to be clear, the writer, who has complete knowledge of the subject, may need clarification from you. It is at that point that you would receive a call or email from us.
Writer’s assignment
As soon as the writer has finished, it will be delivered both to the website and to your email address so that you will not miss it. If your deadline is close at hand, we will place a call to you to make sure that you receive the paper on time.
Completing the order and download