For this week’s forum, locate a research article that used an ANOVA and apost-hoc analysis in their methods/results.. Please attach the article or provide a link so classmates can view it. Describe how the ANOVA and post-hoc analysis was used to answer the research (i.e. what did it compare) and where the group differences were found in the post-hoc. Please share the levels of the dependent and independent variable(s). As always, please select an article that no one else has used or discussed for this week.
SPHS500 – Statistics for
Sports and Health Sciences
Week 5
Objectives
• Analysis of Variance (ANOVA)
• One-way ANOVA
• Repeated Measures ANOVA
• Interpreting test results
• Post-hoc tests
ANOVA
• ANOVA is used when more than two groups are compared
• In order to conduct an ANOVA, several assumptions must be made:
• The population from which the samples are drawn are normally distributed
• The populations from which the samples are drawn have equal variances
• Some ask – why not multiple t-tests?
• That increases the likelihood of a Type I error
Decision Table for Inferential Statistic
Normal deviate z-test
One sample t-test
Independent t-test
Dependent t-test
One-way ANOVA and
post hoc test
Not covered
Factorial ANOVA
Not covered
Chi-square goodness of fit
Chi-square independence
Pearson r
Not covered
One Way (Between subjects) ANOVA
• Single independent variable
• IV = depression level
• 3 levels (medication, counseling, diet supplement)
ANOVA
Analysis of Variance:
• Used with a quantitative Dependent Variable
• Comparison among 3 or more groups
• A Between subjects (one-way) ANOVA is when there are 3 different groups
• Freshman, sophomore, junior, senior
• Categories of an Independent Variable (Low, Medium, High)
• A Repeated measures ANOVA is when the same group is compared at
different time points (measures are repeated)
• Baseline, 3-month, 6-month, 9-month, post
Types of variance in an ANOVA:
1. Between-groups variance
• Variance due to differences between the groups (i.e., between the
factors/levels).
2. Within-groups variance
• Variance due to differences within the groups (i.e., between the individuals).
3. Total variability
• The difference of each score from the grand mean (actually the squared
difference)
The F-Ratio
Between-subjects variability
F=
Within-subjects variability
Treatment effect + Indiv. Diff. + Exper. Error
F=
Indiv. Diff. + Exper. Error
The F-ratio
F=
Between-subjects variability
Within-subjects variability
Variance = Mean Square (MS) in ANOVA since variance is the
mean of the squared deviation scores
• For each source find:
• Sum of squares (Between-groups, Within-groups, Total)
• Degrees of freedom
• Compute Mean Sum of Squares
• F = MSB / MSW = (SSB / dfB) / (SSW / dfW)
Let’s walk through an example:
Do mini-golfers play better (i.e. lower score) using
a white, blue or red ball (3 different groups)?
Red
White
Blue
3
6
4
5
3
8
2
7
7
3
1
5
4
4
5
• What are your null and alternate hypotheses?
Our hypotheses
• Null hypothesis – there is no difference between the
means for the three different groups
• Ho: μ1 = μ2 = μ3
• example, Group 1 = Group 2 = Group 3
• Alternate hypothesis
• ANOVA is omnibus – tests for an overall difference between
means (neither one nor two-tailed)
• HA: X1 ≠ X2 ≠ … ≠ Xk
• HA: at least one of the means is different
Compute Sum of Squares
Red Ball (n1=5)
White Ball (n2=5)
Blue Ball (n3=10)
TOTAL (N=15) (k=3)
3
6
4
5
3
8
2
7
7
3
1
5
4
4
5
X =3.4
X = 4.2
X = 5.8
∑X = 17
∑X = 21
∑X = 29
∑(∑X) = 67
∑(X2) = 63
∑(X2) = 111
∑(X2) = 179
∑(∑ (X2)) = 353
Compute Sum of Squares
Red Ball (n1=5)
White Ball (n2=5)
Blue Ball (n3=5)
TOTAL (N=15) (k=3)
X = 3.4
X = 4.2
X = 5.8
∑X = 17
∑X = 21
∑X = 29
∑(∑X) = 67
∑(X2) = 63
∑(X2) = 111
∑(X2) = 179
∑(∑ (X2)) = 353
67 ) 2
((X )) 2
(2534
353
53.7 .5
SStot = (( X )) −
= 216910
−
= 2871
N
1530
sum of the scores in the column)2
((X )) 2
SSb = (
)−(
)
n of the scores in the column
N
21 2
29 2
53.7 ) 2
17 2
(766)
(852)
(916)
(2534
= (
+
+
)−(
)
10
30
510
15
5
510
= 1133.1
14.93
2
53.7 – 1133.1
14.93
38.8
SSw = SStot – SSb = 2871.5
= 1738.4
Essay Writing Service Features
Our Experience
No matter how complex your assignment is, we can find the right professional for your specific task. Achiever Papers is an essay writing company that hires only the smartest minds to help you with your projects. Our expertise allows us to provide students with high-quality academic writing, editing & proofreading services.
Free Features
Free revision policy
$10Free bibliography & reference
$8Free title page
$8Free formatting
$8How Our Dissertation Writing Service Works
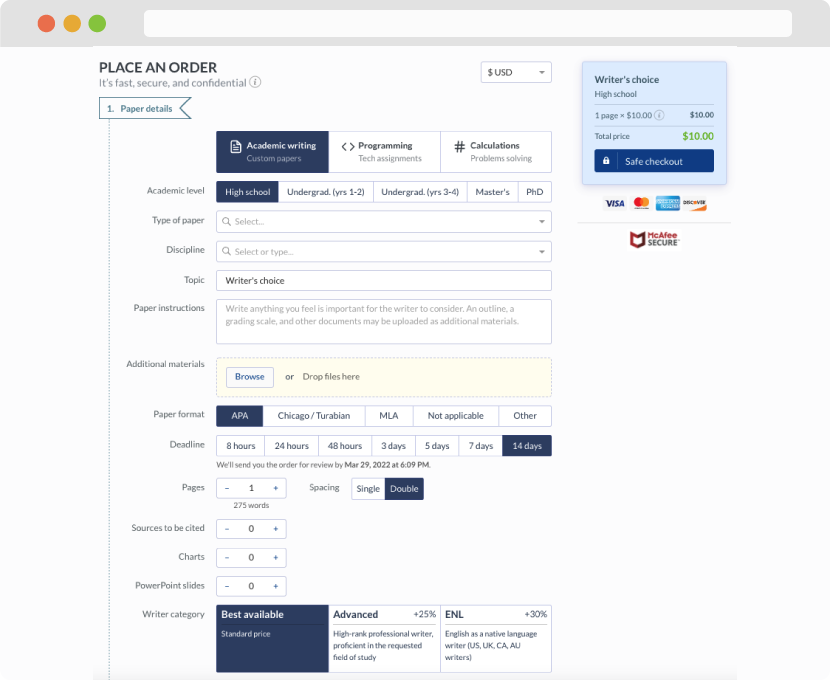
First, you will need to complete an order form. It's not difficult but, if anything is unclear, you may always chat with us so that we can guide you through it. On the order form, you will need to include some basic information concerning your order: subject, topic, number of pages, etc. We also encourage our clients to upload any relevant information or sources that will help.
Complete the order form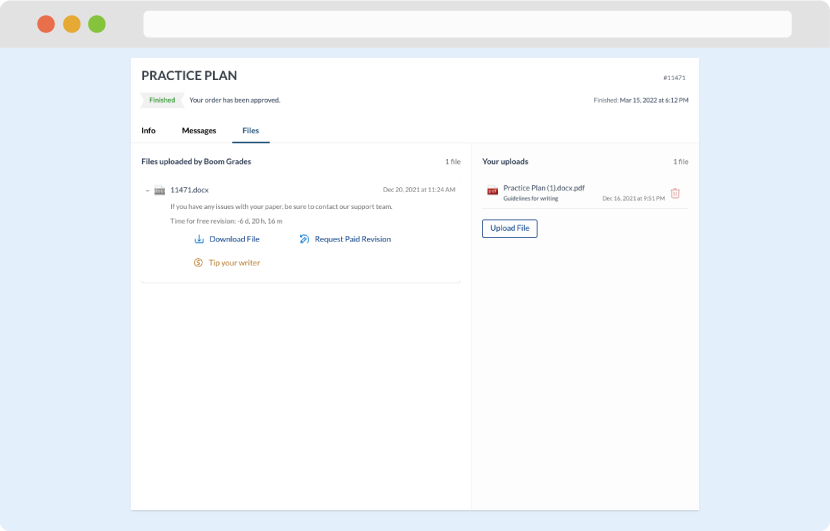
Once we have all the information and instructions that we need, we select the most suitable writer for your assignment. While everything seems to be clear, the writer, who has complete knowledge of the subject, may need clarification from you. It is at that point that you would receive a call or email from us.
Writer’s assignment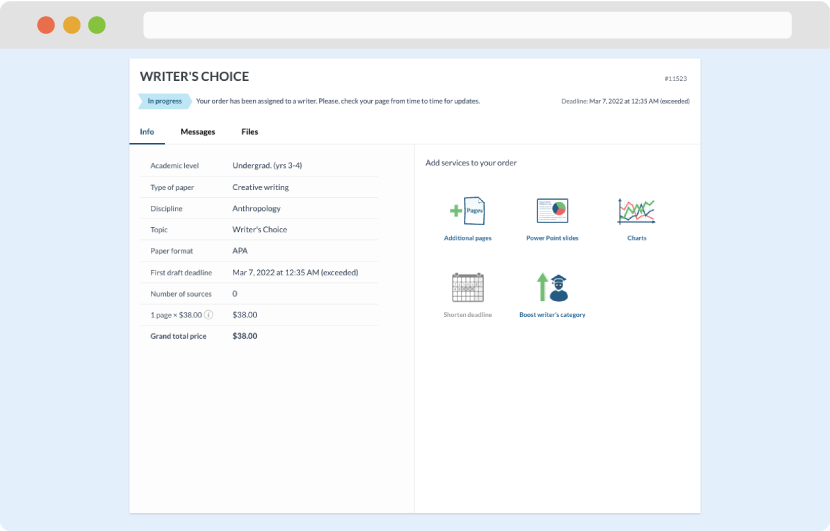
As soon as the writer has finished, it will be delivered both to the website and to your email address so that you will not miss it. If your deadline is close at hand, we will place a call to you to make sure that you receive the paper on time.
Completing the order and download